Presentazione
Nel 1996 ho tenuto un corso che, nella sua prima parte, riprendeva i temi del mio saggio "Riflessioni sul luogo" contenuto ne "La notte dei lampi". In particolare si è discusso sui solidi platonici, utilizzando come sintesi conclusiva dei materiali grafici. Questa discussione è stata ripresa nei miei "Frammenti epistemologici", cap. III (pp. 52 sgg.) intitolato "Sui quattro bellissimi corpi". A questo capitolo si rimanda per le spiegazioni e i commenti alle immagini qui proposte. Oltre ai titoli, alcune note e citazioni tracciano un percorso minimo. Non manca poi qualche divertimento grafico. [G.P., 1918]
1. Dal triangolo equilatero al triangolo “elementare” di Platone.
2. Il triangolo equilatero consta di sei triangoli elementari platonici.
5. Il dodecaedro consta di dodici facce pentagonali. Passi della triangolazione.
6. Relazione tra il dodecaedro e l’icosaedro.
7. Relazione tra il dodecaedro e il cubo.
8. Sui poliedri platonici e la sfera.
1. Dal triangolo equilatero al triangolo “elementare” di Platone
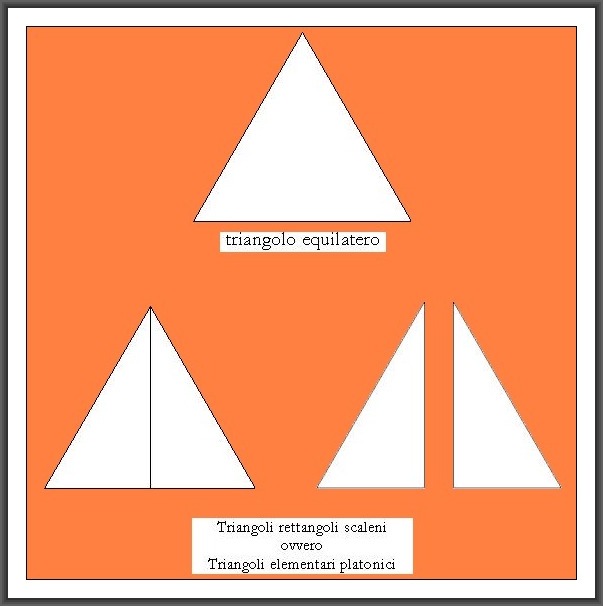
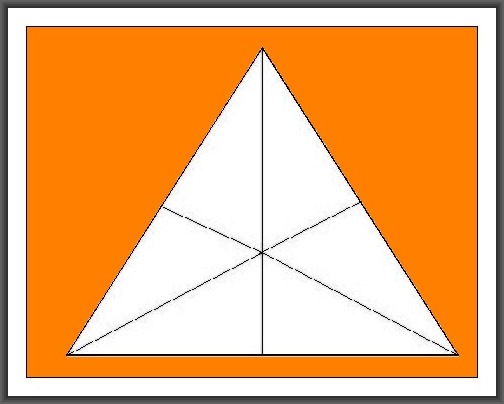
2. Il triangolo equilatero consta di sei triangoli elementari platonici
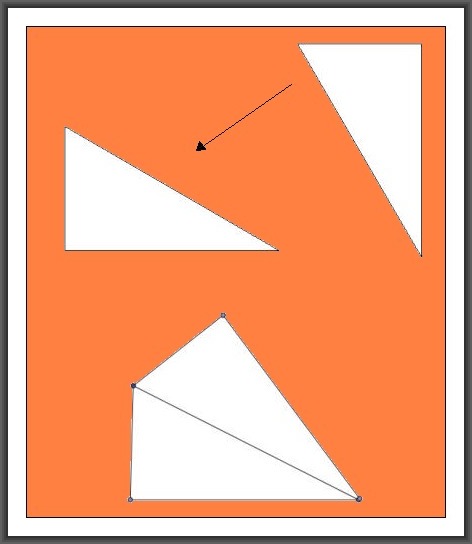

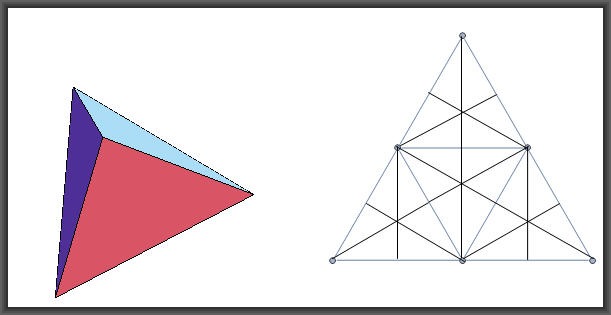
3. Le facce dei poliedri tetraedro, ottaedro, icosaedro constano tutte di triangoli equilateri, e quindi sono divisibili in triangoli elementari platonici.
Tetraedro = Fuoco
Ottaedro = Aria
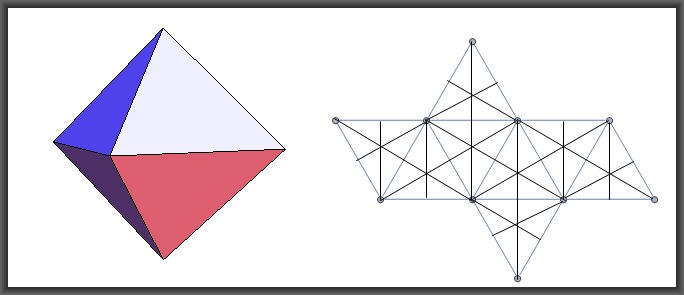
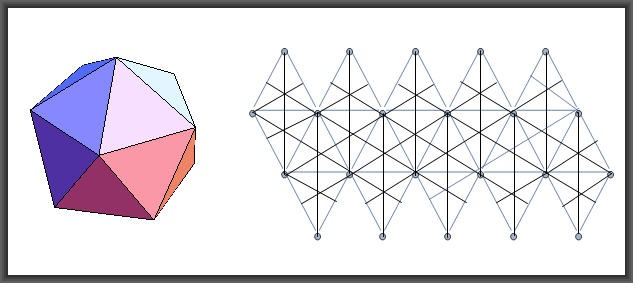
Icosaedro = Aria
4. L’esaedro (cubo) consta di sei facce quadrate, divisibili solo in triangoli isosceli attraverso le diagonali.
Esaedro = Terra
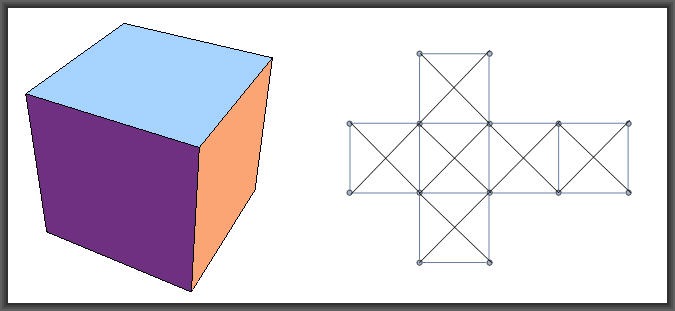
Nota:
Il cubo si trova tuttavia in relazione con il tetraedro, perché il tetraedro può essere inscritto nel cubo “ma non in modo tale da mostrare uno dei lati triangolari sulla faccia del cubo; ciascuno spigolo del tetraedro appare come diagonale di una faccia quadrata del cubo. Il quadrato, in ogni caso, è presente come base mediana delle piramidi di triangoli equilateri che formano l’ottaedro; e due piramidi di triangoli equilateri con basi pentagonali sono impiegati nella costruzione dell’icosaedro”.
R. F. Kotrc, The dodecahedron in Plato’s Timaeus, in «Rheinischen Museum für Philologie», 1981, p. 218. Si trova all’indirizzo internet: http://rhm.phil-fak.uni-koeln.de/1980-1989.html#124
5. Il dodecaedro consta di dodici facce pentagonali. Passi della triangolazione.
Dodecaedro = il Tutto
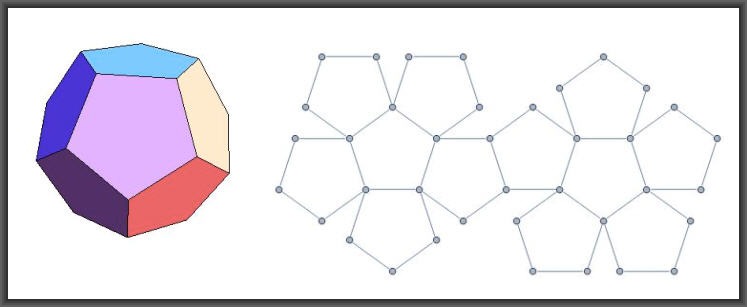
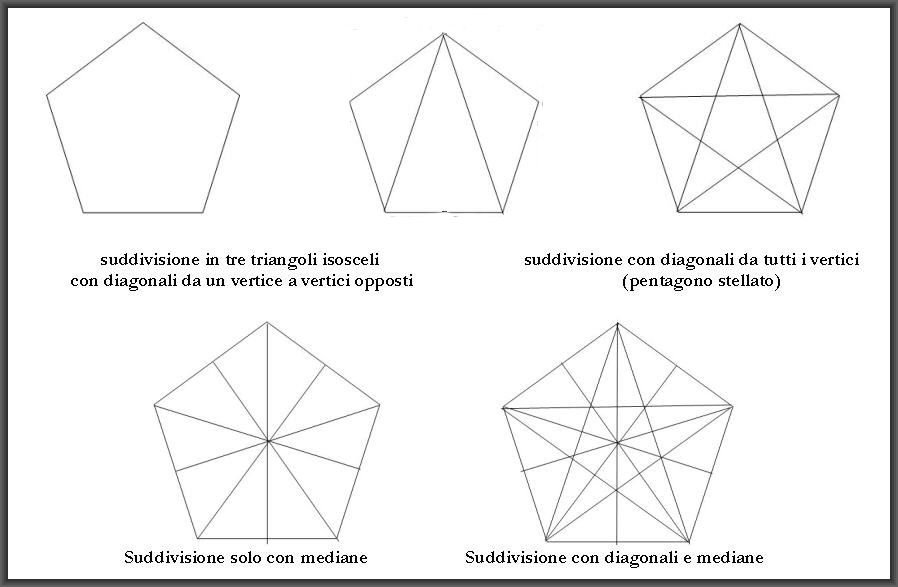
Nota:
Il pentagono può essere suddiviso in trenta triangoli rettangoli scaleni che non sono però triangoli “platonici” (P. Cromwell, Polyhedra, Cambridge 1999, p. 54). Per ottenere triangoli equilateri e quindi triangoli scaleni platonici è necessaria l’ “elevazione” nella misura opportuna del centro del pentagono. La figura che ne risulta è detta “dodecaedro stellato”. Il punto essenziale è in ogni caso la triangolazione in 360 triangoli rettangoli. Platone non considera poliedri "stellati" che saranno in seguito oggetto di attenzione e di studio approfondito da parte di Keplero.
Dodecaedro Stellato

6. Relazione tra il dodecaedro e l’icosaedro

Il pentagono è visibile sulla superficie dell’icosaedro
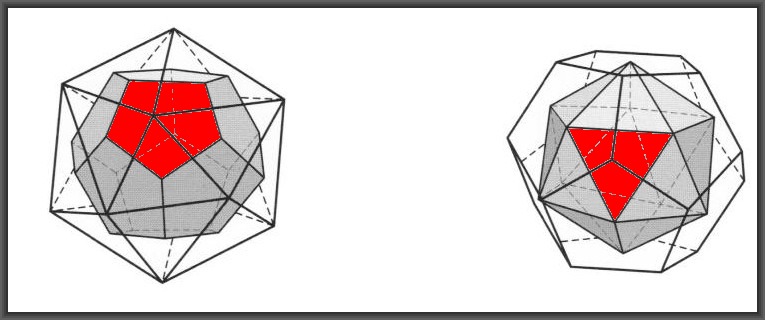
“Dualità” tra dodecaedro e icosaedro
Connettendo i centri di tutte le facce adiacenti
di un icosaedro, si ottiene un dodecaedro. E inversamente.
7. Relazione tra il dodecaedro e il cubo
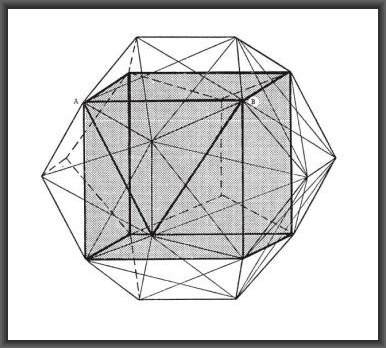
Nota:
“Il cubo può facilmente essere inscritto nel dodecaedro, essendo una linea di ciascuno dei dodici pentagrammi utilissata nella sua formazione. È importante notare che nessuna delle sei superfici del cubo giace su una delle superfici piane del dodecaedro in cui esso è inscritto. Analogamente, il triangolo equilatero appare sulla superficie del dodecaedro quando il pentagramma è disegnato su ciascuna delle facce pentagonali. Il triangolo non appare su un piano ma piuttosto come base di tre tre piani contigui che formano un angolo solido; esso ha una relazione con il dodecaedro simile a quella del cubo: uno dei lati del triangolo diventa la stessa linea del pentagramma usato per iscrivere il cubo (linea A–B)”. (Kotrc, cit. p. 220–1). Sulla base della “dualità” tra dodecaedro e icosaedro e di queste ultime considerazioni Kotrc può concludere rilevando la presenza nel dodecaedro di tutti gli elementi costitutivi dei solidi platonici, fornendo nello stesso tempo un’ interpretazione originale del riferimento simbolico alla totalità: “… il punto importante è che quando i pentagrammi sono stati disegnati sulle facce pentagonali del dodecaedro, si possono chiaramente vedere sia il cubo (e quindi il triangolo rettangolo isoscele) e il triangolo equilatero. Di conseguenza la frase “to pan” ha un significato più ampio rispetto alla prossimità del dodecaedro alla sfera: visibilmente esso incorpora in stesso tutte le superficie che combina e ricombina per formare gli altri quattro solidi regolari della fisica platonica. Così facendo, esso costituisce una matrice geometrica nella formazione dell’universo fisico” (ivi)
Tenendo conto di queste considerazioni mi azzardo a proporre una figura che mi sembra più evidente di quella proposta da Kotrc.
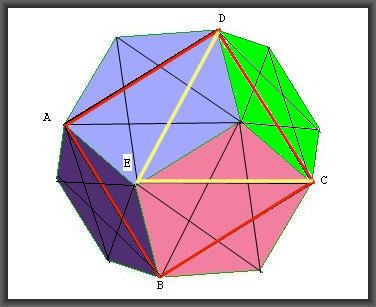
In rosso sono contrassegnati i lati di una faccia ABCD del cubo inscritto. In nero sono disegnati i pentagrammi sulle facce pentagonali del dodecaedro. Ciascun lato del quadrato coincide con un lato del pentagramma e questo è di conse-guenza “coperto” dal rosso. I lati del triangolo EDC a loro volta dovrebbero essere disegnati in giallo ma uno dei essi è “coperto” dal rosso del quadrato. Il triangolo EDC è equilatero essendo ADE ed ECB isosceli, e dunque i lati EC ed ED entrambi eguali al lato del quadrato CD.
8. Sui poliedri platonici e la sfera.

Tutti i poliedri regolari possono essere inscritti o circoscritti ad una sfera
e inversamente







Approssimazione alla sfera del dodecaedro stellato
8. Digressione Kepleriana
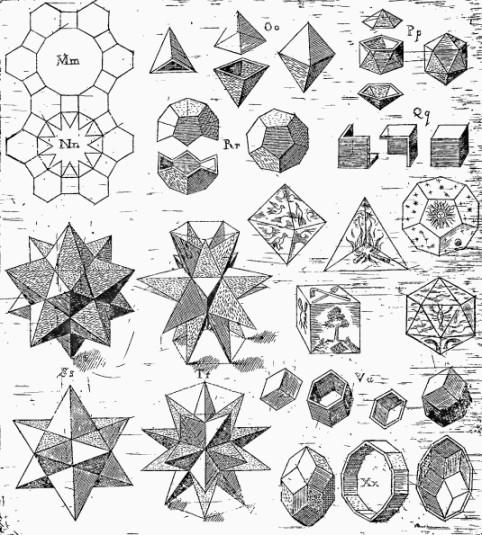
Kepler, Harmonices mundi (1619), p. 57

Kepler, Harmonices mundi, p. 57, part.
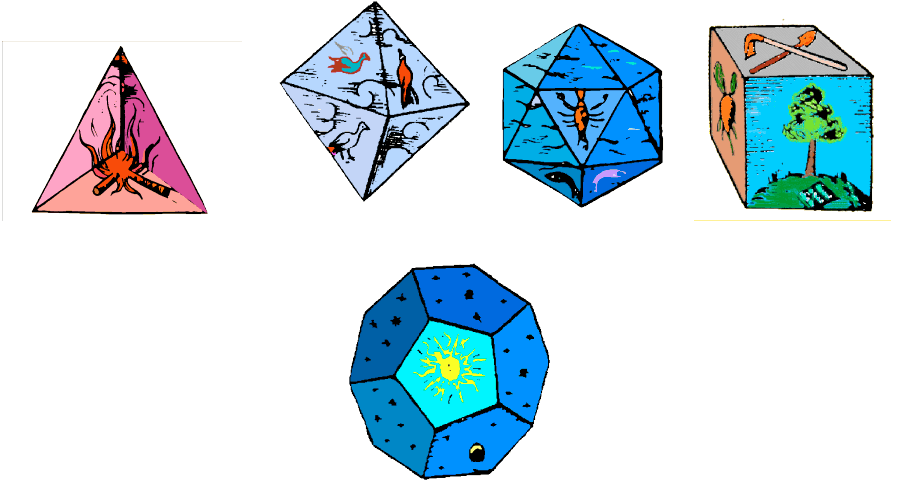
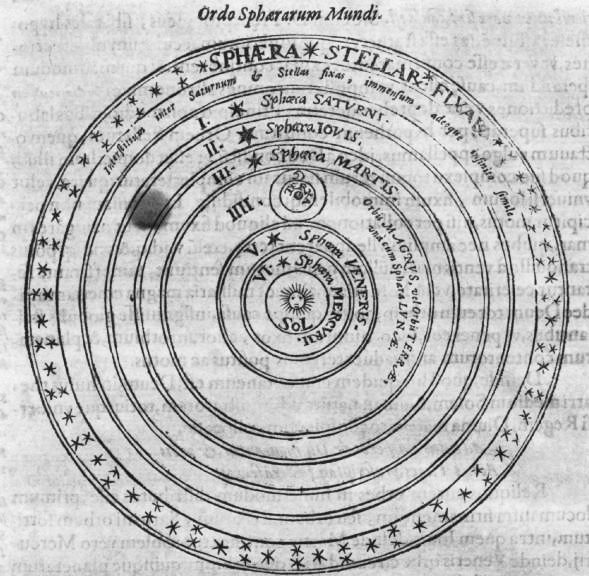
Kepler, Mysterium Cosmographicum (1595), p. 112
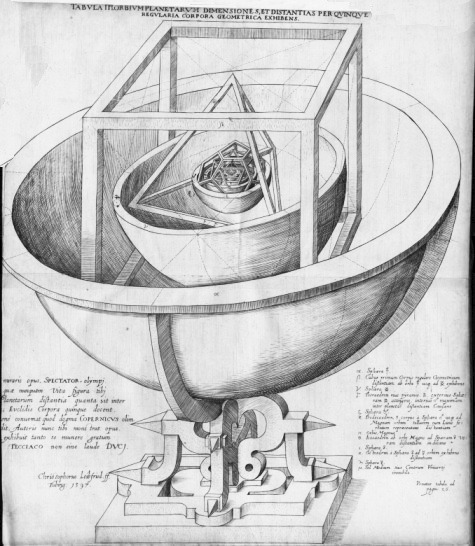
Kepler, Mysterium Cosmographicum (1595), p. 25
Nota:
Al tempo in cui scrisse il Mysterium cosmographicum (1595), Keplero era già sostenitore del sistema copernicano ma non aveva ancora studiato il problema delle orbite ed era lontano dal sospettare che essere fossero ellittiche. Inoltre va rammentato che i pianeti allora riconosciuti erano sei: nell’ordine di distanza dal Sole, considerato, a partire da Copernico, al centro dell’universo: Saturno, Giove, Marte, Terra, Venere, Mercurio.
Ora la domanda di Keplero era: “Perché sei pianeti invece che venti o cento?” Domanda assai singolare che tuttavia mostra già in se stessa un atteggiamento platonico-matematizzante: da un punto di vista geometrico, se io ad esempio dico, vi sono solo cinque solidi regolari, debbo darne la dimostrazione, dobbiamo di questa circostanza dare una giustificazione intrinseca. Affrontando la questione del numero dei pianeti con un atteggiamento matematizzante sembra del tutto naturale chiedersi perché sei e non più di sei pianeti. L’esempio dei poliedri sostiene il primo passo per dare una risposta a questa domanda. Poiché abbiamo già la dimostrazione euclidea che i poliedri regolari sono solo cinque possiamo forse appoggiarci su di essa, correlando i pianeti ai solidi regolari per trovare una giustificazione logica profonda. In questo modo la “necessità” relativa al numero dei poliedri regolari, dimostrata da Euclide, avrebbe potuto essere trasferita direttamente anche al numero dei pianeti. Ma in che modo può essere posta una simile correlazione? E possiamo realmente venire a capo intanto del semplice fatto che i pianeti sono sei e i poliedri regolari sono cinque? Intanto vi è una relazione tra poliedri e pianeti per una precisa ragione formale – e cioè il rapporto con la sfera. Keplero non pensa tuttavia tanto alla forma sferica dei pianeti quanto alla forma circolare delle orbite dei pianeti. Questa forma circolare era allora rappresentata dall’idea che il pianeta fosse innestato su una sfera celeste in movimento: invece di pensare al corpo in movimento circolare nel vuoto, lo pensiamo come “fissato” su una sfera che ruota su stessa, e che quindi fa compiere al pianeta un moto circolare. Ora, tutte le nostre immagini precedenti illustravano che una sfera può essere circoscritta ad un poliedro ed essere inscritta in esso. Proprio sviluppando l’idea di un simile rapporto di inscritto e circoscritto riusciamo ad afferrare l’intenzione di principio che guida la considerazione di Keplero e che rende conto dell’immagine proposta nel Mysterium Cosmographicum. Essa non è da intendere come una rappresentazione fisica vera e propria; e nemmeno hanno una parte rilevante le associazioni immaginative. Certo, qui Keplero ha di fronte un mistero, parola che compare nel titolo dell’opera, e cerca di penetrarlo con uno sforzo dell’immaginazione, ma questa immaginazione è volta in direzione di scoprire una relazione logica e metterla alla prova in rapporto a fatti di ordine fisico. Beninteso, Keplero non rinuncia in ogni caso ad approfittare della simbologia del poliedri per accennare a considerazioni astrologiche relativamente ai singoli pianeti.
Nella figura vediamo alternarsi sfera e poliedro, secondo il rapporto inscritto-circoscritto. Prendiamo le msse da una sfera circoscritta ad un cubo. Cominciamo dunque a contare una sfera, e quindi un pianeta. Si tratterà propriamente di Saturno. Il raggio della sfera coincide naturalmente con la distanza dal sole di Saturno. Poi vi sarà una sfera inscritta nel cubo e circoscritta ad un tetraedro. A ciò corrisponde una seconda sfera e un secondo pianeta (Giove). Poi vi sarà una sfera inscritta al tetraedro e circoscritta al dodecaedro. Terza sfera, terzo pianeta (Marte). Quindi: una sfera inscritta al dodecaedro e circoscritta all’icosaedro. Quarta sfera, quarto pianeta (Terra). Ed ancora: una sfera inscritta nell’icosaedro e circoscritta all’ottaedro. Quinta sfera, quinto pianeta (Venere) . Infine vi sarà una sfera inscritta nell’ottaedro. E questa è la sesta sfera e dunque il sesto pianeta (Mercurio). I conti tornano. E il ragionamento consiste fondamentalmente nel contare tutte le possibilità di sfere circoscritte ad un poliedro regolare e inscritte in esso. Queste sfere sono esattamente sei come sono cinque i poliedri regolari. Non abbiamo un settimo poliedro da circoscrivere alla sfera più esterna, oppure da inscrivere nella sfera più interna. Nello stesso tempo queste sfere ovvero queste orbite hanno certamente un preciso rapporto matematico tra loro, le varie orbite sono messe in relazione secondo un principio unitario e assolutamente “ferreo”. Da notare che nonostante la corposità del modello che viene qui disegnato, che sembra anche un congegno che si può mettere in moto, Keplero non ha evidentemente bisogno di assumere che tra un orbita e l’altra ci sia realmente un poliedro, e per di più vacuum come viene disegnato qui, un enorme poliedro fatto con dei listelloni. Ciò che interessa è, nonostante la fantasiosità del modello, proprio il rapporto logico. La via platonica continua qui in ogni senso, continua nei suoi ragionamenti geometrici, logici, razionali, e nei suoi ragionamenti “bastardi”. Di lì a poco, comunque, Keplero enuncerà le sue leggi sul moto ellittico dei pianeti, e naturalmente rinuncerà al modello proposto nel Mysterium. Tuttavia continuerà a ricercare delle motivazioni assolute, pensando piuttosto ad una concezione puramente aritmetica dell’armonia dei moti planetari. In quest’ultima fase della sua speculazione pensa soprattutto a spiegazioni che hanno un filo conduttore musicale.
Vai all'indice
