Questo testo è stato pubblicato dalla «Rivista Italiana di Musicologia» XXXVI, 2001, n. 2
Versione digitale: 2003
![]() Giovanni Piana, La scala universale dei suoni di Daniélou (398.64 kB) (pp. 51)
Giovanni Piana, La scala universale dei suoni di Daniélou (398.64 kB) (pp. 51)
Giovanni Piana
La scala universale dei suoni di Daniélou
Indice
1. L’idea di scala naturale e la critica di una fondazione negli armonici
2. La partizione degli intervalli primitivi come metodo per la formazione di una «scala universale»
3. Scala «ciclica» e «scala universale»
4. Digressione neopitagorica e la mente come calcolatore
5. La derivazione calcolistica della scala universale
6. La formula che sta alla base della scala universale

1. L'idea di scala naturale e la critica di una fondazione negli armonici
Non vi è dubbio che uno degli argomenti considerati immediatamente probanti contro le istanze di fondazione naturalistica possa essere rappresentato dalla semplice esibizione della molteplicità di strutture intervallari che possiamo trovare in culture musicali evolute lontane dalla tradizione musicale europea - come quella indiana, cinese, giapponese o araba. Si potrà allora subito porre l'accento sul relativismo culturale e sulla necessità di adottare un punto di vista convenzionalistico in rapporto al problema delle possibili suddivisioni dell'ottava. Un simile punto di vista è dato spesso per scontato proprio su questa base. Sembra che si debba dare come altrettanto scontato il nesso tra linguaggio tonale e fondazione naturalistica, cosicché se il linguaggio tonale cessa di essere difeso come il linguaggio «migliore», verrebbe a cadere ogni problema di fondazione naturalistica, o più in generale oggettivistica. Eppure proprio la teoria novecentesca della musica non conferma ovunque e in modo unanime questi luoghi comuni - la controversia sulla «naturalità» va ben oltre le soglie del secolo ventesimo e arriva a ricomprendere anche la molteplicità linguistica che può essere considerata uno dei punti solidamente acquisiti [1] . Così, se andiamo a vedere come stanno le cose presso uno studioso come Alain Daniélou, che si è guadagnato grandissimi meriti come critico di una concezione eurocentrica della musica e come promotore della musica orientale in genere e indiana in particolare, troviamo una posizione assai diversa, assai più articolata. Certamente ci tratta di un autore che può suscitare accese idiosincrasie - ed è facile disfarsi di lui con un'alzata di spalle: tuttavia forse è tempo, proprio ora che guardiamo al novecento come al nostro passato, di disfarsi invece proprio delle nostre idiosincrasie per tentare pacatamente di comprendere quali siano i pensieri e gli umori che hanno attraversato la ricchissima vicenda della musicalità novecentesca.
Anzitutto per Daniélou non vi è alcun problema nell'ammissione della molteplicità delle scale. Basta, egli dice ad un certo punto nel suo volume Introduction to the study of musical Scales [2] con la storia del buon selvaggio che raccoglie la canna da terra e che scopre così la scala diatonica che Zarlino supponeva fosse «la scala naturale». Invece bisogna rendersi conto che vi sono «migliaia di scale che sono possibili, espressive, piacevoli all'orecchio e perfettamente naturali e legittime» [3]. Ma questa affermazione non è orientata in senso relativistico e prepara anzi una complicata elaborazione per mostrare che vi è una unica possibile suddivisione dello spazio sonoro dell'ottava che possa essere chiamata «naturale»: essa rappresenta una sorta di trama fondamentale di intervalli che vengono variamente selezionati dando luogo appunto ad un'amplissima molteplicità di scale, che sono «piacevoli all'orecchio e perfettamente naturali e legittime» proprio per il fatto che poggiano su di essa. Da queste scale si distingueranno poi strutture scalari «artificiali» - dipendenti da suddivisione arbitrarie (innaturali) - che saranno appunto prive di giustificazioni, ed assai dubbie dal punto di vista musicale.
L'idea guida piuttosto semplice è la seguente: quanto più è fine una suddivisione dell'ottava che si possa chiamare naturale, tanto più numerosi saranno i sistemi linguistici che, fondandosi su di essa, potranno essere caratterizzati a loro volta come naturali. Così come assumendo un'ottava divisa in dodici parti potremmo rendere conto di un numero molto ampio di sistemi scalari possibili, molto al di là dei modi maggiore e minore, questa possibilità di giustificazione si estenderà a dismisura, aumentando la finezza della suddivisione. In questo modo si toglie subito di mezzo l'equivoco che considera immediato il passaggio da una molteplicità di sistemi musicali ad una posizione accentuata di relativismo culturale. Sullo sfondo vi è l'idea dell'unità profonda soggiacente alla molteplicità dei linguaggi della musica. La tesi di Daniélou è infatti che «i differenti sistemi musicali non si oppongono l'un l'altro, ma al contrario si completano vicendevolmente, in quanto essi scaturiscono necessariamente dalle stesse leggi fondamentali di cui sfruttano aspetti differenti» [4].
Ma il problema è evidentemente: secondo quale procedura potremo aumentare la finezza della suddivisione tenendo conto della condizione essenziale che qualunque proposta debba essere non-arbitraria, e quindi debba essere realizzata secondo un metodo che ne garantisca la «naturalità»? Forse in luogo di «naturalità» si potrebbe anche dire «naturalezza» - che certamente presenta una diversa inclinazione di senso. La prima la potremmo riservare per un richiamo alla natura fisica in senso forte, mentre la seconda, come nell'uso comune, riguarda piuttosto l'assenza di forzature, come quando parliamo di una posizione naturale del corpo contrapponendola ad una posizione forzata. Nel caso di Daniélou, potrebbero essere impiegati entrambi i termini, tenendo conto tuttavia che parlando di naturalità e dunque anche di naturalismo ci si orienta verso un tentativo di fondazione psico-fisiologica, piuttosto che fisicalistica.
Da questo punto di vista è significativa la presa di posizione molto chiara da parte di Daniélou contro l'idea ogni tematica fondativa debba ricorrere agli armonici dei suoni, e in particolare che essi siano da chiamare in causa per fornire una partizione «valida» dello spazio sonoro. Già per questo motivo la sua posizione assume un proprio inconsueto profilo.
Partecipando ad un Colloquio intitolato «Gli elementi della formazione delle scale al di fuori della 'risonanza' - le deformazioni espressive» [5] - dove il termine «résonance» sta appunto ad indicare il fenomeno degli armonici, in apertura del proprio intervento, egli protesta vivacemente nei confronti del titolo, proposto da Chailley, organizzatore del colloquio. In esso - e su questo Daniélou ha perfettamente ragione - vi è una tesi implicita secondo la quale esisterebbe uno schema intervallare «normale», «naturale», che è quello fondato negli armonici, e tutte le altre scale dovrebbero essere interpretate come deviazioni da quello schema, come sue «deformazioni» dovute ad intenzioni di enfatizzazione, di accentuazione e di esasperazione espressiva. Ho la sensazione di trovarmi - comincia a dire Daniélou - all'interno di un «coro di virtuosi omaggi agli armonici» (dans un concert des vertueux hommages aux harmoniques), ma nei panni di un accusato sospettato di deviare l'attenzione verso intervalli minori - forse si può tradurre in questo modo il vivace gioco di parole dell'espressione Détournements d'intervalles mineurs, essendo détournement des mineurs la «corruzione di minorenni». In altri termini: non mi adeguo ad una interpretazione nella quale la virtù della musica sta nella virtù degli armonici, e di fronte a ciò preferisco fare la parte del corruttore, attirando l'attenzione proprio verso quegli intervalli che negli armonici non hanno necessariamente una giustificazione, mentre la hanno nella pratica musicale.
Non vi è dubbio infatti che la posizione di Daniélou voglia essere una posizione che comincia a mettersi dalla parte dei musicisti, con un certo scetticismo per le fondazioni fisiche ed aritmetiche quando queste siano puramente «speculative» e lontane dalla pratica musicale.
Ricollegandosi al titolo del colloquio egli osserva ancora che «Il termine di deformazioni espressive fa pensare a vecchie accuse contro i musicisti che si ostinano a tirare le corde per ottenere suoni differenti dalle giuste intonazioni» [6]. Nello studio degli intervalli musicali - continua Daniélou - si sono per lo più cercate giustificazioni fisico-aritmetiche proponendo sistemi per rendere conto delle pratiche musicali sugli intervalli, e «tuttavia noi osserviamo sempre presso i teorici la stessa irritazione davanti al fatto che i musicisti, e soprattutto i migliori, non sembra si conformino esattamente agli intervalli di alcun sistema». Non è il caso allora di chiedersi se queste variazioni possano essere realmente caratterizzate come «deformazioni» oppure esse non siano «al contrario degli elementi fondamentali del vocabolario musicale»? [7].
Vi sono del resto dei motivi strettamente musicali alla base di questa presa di posizione di Daniélou che riguardano proprio la sua attenzione verso la musica orientale e verso la musica indiana. Una delle differenze particolarmente importanti rispetto alla tradizione del linguaggio tonale europeo sta nell'elemento armonico, nel senso particolare che questo termine detiene in riferimento a questo linguaggio: armonia vuol dire armonia triadica, vuol dire rilevanza della relazione con la quinta e suo speciale uso, vuol dire tendenziale compressione dell'elemento melodico, riduzione e restrizione del modo a favore del tono, vuol dire dominio del modo maggiore. Le propensioni musicali di Daniélou sono invece dirette verso una rivalutazione della modalità - e quindi verso una considerazione che mette l'accento sulla libertà e sulla varietà del melos. In questa prospettiva è semmai l'elemento verticale che deve subordinarsi a quello orizzontale piuttosto che inversamente. L'idea che siano le figure melodiche - e quindi un determinato schema intervallare - a determinare l'armonia, è esplicitamente formulata da Daniélou [8] .
Ora una concezione tutta puntata sugli armonici porterebbe indubbiamente ad una valorizzazione indebita dell'armonia tonale e del modo di configurare il rapporto armonia-melodia tipico del linguaggio tonale. Proprio su questo punto si può notare quanto sia mutato, nella sua ripresa novecentesca, il problema di una fondazione oggettiva, che nelle sue formulazioni ottocentesche difficilmente riusciva a liberarsi da una relazione intrinseca con il linguaggio tonale. Possiamo dare per incontestabile il fatto che l'armonia tonale abbia come architettura fondamentale la triade maggiore; ed altrettanto incontestabile è il fatto fisico che i primi armonici del suono singolo diano evidenza ad essa. Ma non necessariamente questi due fatti si trovano in connessione tale per cui il secondo - il dato di fatto fisico-acustico - stia a fondamento e quindi a giustificazione del dato di fatto musicale. Daniélou propone invece un geniale rovesciamento di punto di vista. È possibile infatti interpretare la semplificazione dei modi nella musica occidentale e il prevalere del modo maggiore come una scelta anzitutto di ordine musicale: questa scelta tuttavia attrae l'attenzione uditiva sugli armonici del suono e viene al tempo stesso da essi accentuata, stimolata e promossa. Fatto fisico e fatto linguistico interagiscono tra loro e si rafforzano l'un l'altro. Man mano che si attenua la sensibilità per l'afferramento delle strutture modali, l'orecchio musicale tende in certo senso a fisicalizzarsi: e ciò significa corrispondentemente che si rafforza la sensibilità verso i primi armonici del suono con la formazione di attese conseguenti sul piano musicale. Ora è chiaro che se interpretiamo le cose in questo modo la funzione fondazionale della teoria degli armonici rispetto alla teoria della tonalità viene quasi completamente meno, e il momento fisico-acustico diventa un momento interno ad una scelta linguistica. In breve potremmo dire che la tonalità è quel linguaggio nel quale assumono importanza i primi armonici del suono. Da questa formulazione tuttavia non possiamo assolutamente trarre la conseguenza che il linguaggio tonale, e la struttura scalare che sta alla sua base, sia l'unico linguaggio fondato dal punto di vista oggettivo e «naturale». L'orecchio è divenuto particolarmente sensibile alla struttura fisica del suono e l'occidente, per affermare l'accordo che riproduce i primi armonici, ha sacrificato «tutte le possibilità dei modi, tanto differenti l'uno dall'altro nella loro struttura e nella loro possibilità quanto lo è un quadrato da un circolo, da un triangolo o da un poligono stellato» [9]. Purtroppo la genialità di questo spostamento di accento è alquanto guastato dalla paccottiglia teorica che fa dire a Daniélou non solo che il modo maggiore non è affatto più «naturale» di altri ed è meno gradevole ed espressivo (e fin qui si potrebbe addirittura convenire!), ma anche che «quando studiamo il simbolismo e le corrispondenze emozionali secondo la teoria indiana, ci rendiamo conto che gli intervalli del modo maggiore sono quelli che indicano egoismo, vanità, materialismo e ricerca di piacere, formando così un contesto in cui la mentalità dei nostri tempi si trova interamente a casa» [10]. Ma nell'occuparci di Daniélou, abbiamo deciso una volta per tutte di chiudere tutti e due gli occhi su questi aspetti, in realtà proprio nel tentativo di rendergli la massima giustizia.
Un altro spunto interessante che si può trovare formulato chiaramente nell'intervento al Colloquio è l'importanza data anche in rapporto a questo ordine di problemi alla distinzione tra produzione vocale e produzione strumentale del suono, e quindi tra una riflessione che faccia prevalentemente leva sull'una o sull'altra. Ciò che Daniélou suggerisce è che vi è presumibilmente una differenza tra una melodia cantata o comunque pensata vocalmente ed i suoi intervalli caratteristici e la stessa melodia che si cerca di riportare su uno strumento che avrà un'accordatura necessariamente standardizzata. La maggior «naturalezza» sarà certamente dalla parte della melodia vocale perché sarà priva di adattamenti e compromessi che si rendono necessari [11] . Ma il senso di questa osservazione - che in se stessa appare un po' generica [12] - sta invece nel fatto che se la riflessione sulla scala si orienta sugli strumenti e sui metodi di accordatura, si darà particolare importanza a certi intervalli piuttosto che a certi altri - si pensi solo all'intervallo di quinta, di quarta e di ottava. Se tuttavia pensiamo ad una melodia così come si sviluppa «vocalmente» nella nostra mente (Mélodie purement vocale ou mentale) - osserva Daniélou - allora le cose cambiano. Alla domanda «se quegli intervalli abbiano la stessa importanza in una melodia vocale o mentale» si risponderà «enfaticamente: no!». «Una quinta giusta non è ad alcun titolo un intervallo melodico più importante che una seconda maggiore o una terza minore, e il fatto che la seconda sia una quinta della quinta non si riflette nel carattere melodico ed espressivo proprio delle seconde» [13]. Queste considerazioni in realtà possono essere ricongiunte a quelle sugli armonici per due ordini di ragioni: la quinta e l'ottava sono gli armonici più forti del suono; in una pratica di accordatura è richiesta una attenzione particolarmente tesa nei confronti degli armonici. Come conclusione del problema potremmo assumere questa citazione di Daniélou: «Gli armonici certo sono importanti» - ma in realtà come «fenomeno secondario, una curiosa proprietà dei corpi sonori tanto utile quanto lo sono i battimenti per accordare gli strumenti, ma che non basta, senza far intervenire altre proprietà dei suoni, a giustificare la struttura delle scale e dell'espressione melodica» [14].
Note
[1] Le cose dette nell'Introduzione al mio saggio La composizione armonica del suono e la serie delle affinità tonali in Hindemith, pubblicato nella rivista «Sonus», n. 21-22, 2002, pp.118-153 e disponibile anche in «De Musica», Internet 2002, possono valere come premessa generale anche per il presente lavoro.
[2] Il volume è stato pubblicato da The India Society, London 1943. In seguito indicato come Introduction.
[3] ivi, p. 6.
[4] ivi, p. 22.
[5] Colloque La Resonance dans les échelles Musicales. Paris 9 -14 Mai 1960, éd. C.N.R.S. 1963: études rèunies et présentées par Edith Weber.
[6] ivi, p. 208
[7] ivi.
[8] Introduction, p. 23.
[9] ivi, p. 216.
[10] ivi.
[11] Secondo Daniélou il compositore spesso tenderà a «pensare vocalmente", cioè a cantare mentalmente il movimento melodico che poi "cercherà di trascrivere in una scala riferendosi a intervalli strumentali che sembrano loro essere approssimativamente gli stessi di quelli pensati vocalmente", ivi, p. 208.
[12] Che la voce tenda cantare su intervalli «naturali»è in realtà di un luogo comune, in rapporto al quale sembra difficile escogitare un metodo attendibile di verifica, spesso ripetuto dai sostenitori dell'esistenza di una scala naturale.
[13] ivi, p. 209.
[14] ivi.

2. La partizione degli intervalli primitivi come metodo per la formazione di una "scala universale"
Con tutto ciò non abbiamo ancora speso nemmeno una parola intorno al metodo per produrre una partizione fine dell’ottava secondo il progetto precedentemente enunciato. La verità è che se ci attenessimo strettamente ai testi di Daniélou, difficilmente potremmo ottenere qualche indicazione soddisfacente proprio sotto il profilo metodico. Se si è interessati, come noi siamo, più che ai risultati, alle ragioni che conducono ad essi, ci si trova indubbiamente di fronte ad esposizioni che non aiutano ad individuarle con chiarezza. I preliminari sono ben pochi e ci si trova troppo presto di fronte a conteggi ed a tabelle. Eppure, a mio avviso, è possibile almeno ipoteticamente, ma con buon fondamento, ricostruire un percorso che è particolarmente significativo proprio nel modo in cui si dipana. A questo tentativo di ricostruzione vogliamo ora dedicarci, sottolineando due volte il fatto che esso non si trova tal quale nei testi di Daniélou ma che si tratta di una ipotesi interpretativa tutta nostra.
Anzitutto è stato escluso il ricorso agli armonici; ma le ultime considerazioni fanno presagire anche qualche dubbio in rapporto al ciclo delle quinte. Anche attraverso il ciclo delle quinte è possibile ottenere una partizione fine dell’ottava. Come vedremo subito, questa possibilità è destinata ad assolvere una funzione importantissima nell’impostazione di Daniélou, ma non come «via maestra» e nemmeno come via da percorrere fin dall’inizio. Questo per la ragione che abbiamo già segnalato nelle nostre ultime considerazioni: dal punto di vista musicale il ciclo delle quinte è collegato ai metodi di accordatura che possono essere sospettati di introdurre un elemento di artificiosità (rammentiamo che lo strumento, rispetto alla voce, è esso stesso un artificio); inoltre essi conferiscono particolare importanza alla quinta, importanza che viene confermata dal riferimento agli armonici. Ma vi è anche una ragione di ordine generale, che peraltro rappresenta uno dei motivi di forte tensione all’interno dell’impostazione di Daniélou. Dobbiamo notare che, almeno stando alle prime apparenze, mentre Daniélou non ama una fondazione fisica, così anche sembra prendere le distanze da procedure di derivazione puramente matematica. Cosicché il ciclo delle quinte, pur essendo per un verso in stretta connessione con la pratica musicale attraverso le tecniche di accordatura, per un altro verso assomiglia ad una procedura di puro calcolo matematico, trattandosi dell’applicazione di una inflessibile procedura ricorsiva. È certo in ogni caso che in Daniélou vi sia un forte interesse empirico, strettamente legato alle problematica della conoscenza della musica extra-europea e della sua trascrizione e riproduzione corretta.
In particolare, quella che proporrei come prima via verso la partizione dell’ottava potrebbe essere considerata come una via del tutto empirica: se vogliamo stare dalla parte dei musicisti dobbiamo andare a vedere gli intervalli che essi utilizzano, cercando poi di realizzare una partizione che segua un metodo che non si distanzi troppo dalla pratica musicale diretta. Ciò è presto detto, ma tutt’altro che facile da farsi e soprattutto non è facile da farsi senza qualche assunzione pregiudiziale. Ad esempio, non avrebbe affatto senso prendere in considerazione tutti i tipi di intervalli utilizzati: questo sarebbe un compito indeterminato. Ed anche un catalogo di intervalli molto ampio sarebbe insignificante se non fosse realizzato seguendo qualche idea-guida.
Piuttosto che girovagare tra una infinità di intervalli possibili, si tratta come primo passo di identificare delle ricorrenze, delle costanze intervallari che si presentano in linguaggi musicali evoluti. Daniélou pensa prevalentemente oltre che alla tradizione europea precedente all’era del temperamento, alla cultura indiana, araba, cinese e giapponese. E ritiene di poter individuare grandezze intervallari che presentandosi in culture musicali differenti con grandezze sostanzialmente omogenee meritino di essere considerate come «primitive» al fine dell’identificazione di una partizione di base.
Si tratta degli intervalli che potremmo indicare con Tono Grande, Tono Piccolo e Semitono Grande. È peraltro sottinteso che la loro presenza in pratiche musicale differenti rappresenta un indizio forte, se non una garanzia della loro «naturalità».
Queste designazioni sono accompagnate da una precisa indicazione quantitativa in termini di rapporto. Il Tono Grande (TG) viene indicato con il rapporto di 9/8 che è l’antica proporzione pitagorica corrispondente a 204 cents, e quindi un po’ più grande del tono temperato. Il Tono Piccolo (TP) è indicato con il rapporto di 10/9 corrispondente a 182 cents e quindi un po’ più piccolo del tono temperato; infine il Semitono Grande (STG) è indicato con il rapporto di 16/15, corrispondente a 112 cents, e quindi un po più grande del semitono temperato. Naturalmente, mentre abbiamo appena detto che la loro presenza sarebbe attestata in pratiche musicali differenti, non possiamo evitare di sottolineare che si tratta ad ogni buon conto di intervalli ben noti anzitutto alla pratica musicale di tradizione europea.
Il termine di intervalli primitivi che adottiamo attinge naturalmente il suo senso solo all’interno dei nostri scopi. A mio avviso, nello spirito di Daniélou, essi vengono proposti anzitutto come un reperto empirico. È possibile ora proporre una partizione del Tono Grande, che si serva sia degli altri due intervalli primitivi (che sono «contenuti» in esso) sia di intervalli ottenibili come differenze tra intervalli e che potremmo chiamare perciò intervalli differenziali. Si tratta in particolare del comma (cma), del limma (lma) e del semitono piccolo (stp)- secondo terminologie e valori anch’essi ben noti nella tradizione europea. In particolare con comma viene assunto il rapporto 81/80 (ottenibile come differenza tra TG e TP, pari a 22 cents) e con semitono piccolo il rapporto 25/24 (differenza tra TP e STG pari a 70 cents). Come limma viene indicato il rapporto pitagorico 256/243 (differenza tra quarta e ditono pitagorico, pari a 90 cents) [15] . Per quanto riguarda ciò che Daniélou chiama doppio comma, non possiamo far altro che prendere atto di due possibili misure, una che corrisponde a (81/80) (43 cents) ed un’altra che corrisponde a 128/125 (41 cents) (caratterizzeremo quest’ultima con 2cma). Di questa differenza, per quanto minima, è necessario tener conto nell’effettuare i calcoli.
Fatte queste premesse la divisione proposta da Daniélou del Tono grande che contiene implicitamente anche la divisione degli altri intervalli primitivi risulta essere la seguente:

La parte superiore del grafico illustra la suddivisione degli intervalli primitivi realizzata contrassegnando dei punti all’interno dell’intervallo che «distano» dall’uno o dall’altro estremo di un intervallo differenziale secondo un’ordine di simmetria speculare [16] . Per ciò che riguarda l’aspetto calcolistico tuttavia conviene far riferimento alla parte inferiore che integra nello schema il semitono grande e il tono piccolo. Risulta allora la seguente partizione del TG, e conseguentemente del TP e del STG, che qui proponiamo per chiarezza e semplicità in cents:
TG = 22, 41, 70, 90, 112, 134, 161, 182, 204
TP = 22, 41, 70, 90, 112, 134, 161, 182
STG = 22, 41, 70, 90, 112
Le differenze tra intervallo e intervallo risultano essere allora le seguenti:
TG = 22, 19, 29, 20, 22, 22, 27, 21, 22
TP = 22, 19, 29, 20, 22, 22, 27, 21
STG = 22, 19, 29, 20, 22
Si tratta di divisioni ineguali in cui in ogni caso prevale il «comma» (usando questo termine in senso abbastanza ampio da comprendere intervalli compresi tra 19 e 24 cents), con «buchi» (disgiunzioni) ovvero intervalli un po’ più ampi contrassegnati con un asterisco nel nostro grafico - due nel Tono Grande e nel Tono piccolo ed uno nel Semitono Grande [17] . Si tratta dunque di una divisione relativamente omogenea, anche se non costituita di parti eguali.
Il passo seguente alla partizione degli intervalli primitivi richiede una seconda importante assunzione. Come in precedenza abbiamo scelto tre intervalli a titolo di intervalli primitivi su cui operare la partizione, così ora dobbiamo scegliere una scala-tipo in cui questi intervalli sono organizzati. La scala-tipo scelta da Daniélou prevede tre Toni Grandi, due Piccoli e due Semitoni grandi - che è in realtà non è altro che la scala zarliniana.
TG TP STG TG TP TG STG
Daniélou ne parla come «scala diatonica naturale» o «scala delle proporzioni» «considerata come la scala fondamentale della musica europea» [18]. Poiché questa scala copre tutta l’ottava e poiché ogni intervallo che compare in essa è stato già suddiviso, la partizione completa dell’ottava è ormai diventata cosa ovvia. Il numero delle parti dipende dalle partizioni dei singoli intervalli, ovvero 9, 8 e 5 rispettivamente per il TG, il TP e STG. Di conseguenza, facendo le somme, arriviamo al numero 53. Quanto alla distribuzione degli intervalli essa risulta dalla distribuzione delle parti negli intervalli primitivi nella scala-tipo.
«Scala universale dei suoni» ottenuta mediante partizione degli intervalli primitivi
Distanza tra un grado e l’altro:
22, 19, 29, 20, 22, 22, 27, 21, 22, 22, 19, 29, 20, 22, 22, 27, 21, 22, 19, 29, 20, 22, 22, 19, 29, 20, 22, 22, 27, 21, 22, 22, 19, 29, 20, 22, 22, 27, 21, 22, 19, 29, 20, 22, 22, 27, 21, 22, 22, 19, 29, 20, 22
Distanza dalla fondamentale:
22, 41, 70, 90, 112, 134, 161, 182, 204, 226, 245, 274, 294, 316, 338, 365, 386, 408, 427, 456, 476, 498, 520, 539, 568, 588, 610, 632, 659, 680, 702, 724, 743, 772, 792, 814, 836, 863, 884, 906, 925, 954, 974, 996, 1018, 1045, 1066, 1088, 1110, 1129, 1158, 1178, 1200
Ecco dunque quello che, a nostro avviso, è un primo percorso che conduce alla «scala di Daniélou», cioè alla scala divisa in 53 intervalli. Essa viene chiamata in vari modi: semplicemente scala dei suoni, oppure scala armonica, scala modale [19] , scala degli intervalli; ed anche scala universale delle misure e scala universale dei suoni [20] . Come si vede, non interviene nessuna considerazione sul ciclo delle quinte; ed inoltre va notato che non è l’ottava l’oggetto vero e proprio della partizione, ma piuttosto intervalli che non appartengono alla sua articolazione fondamentale in quinta e quarta. È poi indispensabile assumere un modello di distribuzione degli intervalli primitivi nell’ottava, e quindi un modello diatonico della sua partizione. Il punto di vista dominante è manifestamente un punto di vista discretistico, e ciò è naturalmente più che confermato dall’idea di determinare gli intervalli fino all’ultimo cent. Più precisamente, diciamo subito che in Daniélou non di rado accade di imbattersi in impieghi del tutto disinvolti di tolleranze ed arrotondamenti anche piuttosto vistosi: e tuttavia il profilo teorico del suo discorso è dato soprattutto dall’accanimento verso la determinazione esatta degli intervalli. Non è probabilmente sbagliato vedere in questa passione calcolatoria e misurativa un tratto caratteristicamente «europeo», nonostante i numerosi riferimenti indianistici. La quantificazione esatta del piccolo intervallo, ed in generale un punto di vista che non riesce a cogliere la presenza della continuità come fattore espressivo mi sembra quanto mai lontano dallo spirito della musica indiana.
Ma prima di tirare le fila e di tentare una nostra valutazione abbiamo ancora una strada piuttosto lunga da compiere. Anzitutto sono necessarie alcune precisazioni. Abbiamo detto che la scala che abbiamo or ora ottenuta viene chiamata da Daniélou anche scala armonica. Quest’ultimo termine non ha nulla o quasi nulla a che vedere con il significato musicale corrente della parola armonia, con i suoi rimandi alla dimensione delle consonanze e degli accordi. È anzi da sottolineare che non viene fatta nessuna considerazione e nessun impiego dei rapporti consonantici - questi non intervengono in nessun modo nel determinare la partizione dell’ottava. La parola «armonia» rimanda piuttosto ad un uso antico, ad un uso greco quando con questa parola si intenda una struttura intervallare ben disposta, bene ordinata, in cui ogni elemento si innesta nell’altro come parte di un tutto - un ordinamento «armonioso» dunque [21] .L’aggettivo «modale» che talvolta, anche se più di rado, viene utilizzato da Daniélou per caratterizzare questa scala, potrebbe sembrare alquanto improprio e soltanto indicativo dell’interesse verso la modalità che orienta nell’insieme tutta questa problematica, ma forse vi è per esso una spiegazione più sottile, che vedremo tra breve. Daniélou evita invece di parlare di scala cromatica, come avrebbe potuto essere tentato di fare.
Molti dubbi possono essere sollevati sul fatto di parlare di scala. Naturalmente è possibile realizzare una simile successione di suoni scalarmente ordinati. Ma, dal punto di vista di Daniélou, si tratta di una partizione dell’ottava che è una pura costruzione teorica priva di carattere musicale diretto. Essa intende presentare uno schema generale ed assoluto a cui riportare le scale effettivamente usate - e che consente di valutare il loro grado di naturalità o di artificialità. Possiamo concepire le scale come regoli graduati - dove le lineette dei gradi contraddistinguono gli intervalli. Una scala sarà da considerarsi «naturale» se tutti i suoi intervalli coincidono con alcune delle 53 lineette della «scala armonica». Si comprende subito allora che la divisione è abbastanza fine da legittimare una enorme quantità di strutture scalari, e tuttavia la scala armonica non giustificherà affatto tutte le scale possibili o tutte le scale musicalmente impiegate. Vi saranno scale le cui lineette coincideranno solo in parte oppure per nulla affatto con le lineette della scala armonica - e tra queste vi è la naturalmente la nostra scala temperata.
Note
[15] Il comma e il semitono piccolo derivano direttamente da differenze che interessano quegli intervalli che abbiamo chiamati primitivi. Anche il limma potrebbe essere introdotto usando questi intervalli, e precisamente come differenza tra tono grande e semitono grande ottenendo in tal caso un valore in rapporto pari a 135/128 (92 cents). Daniélou segnala anche questo rapporto, ma si serve nella suddivisione degli intervalli «primitivi» del rapporto 256/243 (90 cents).
[16] Secondo questo tipo di divisione anche il tono piccolo e il semitono vengono ripartiti simmetricamente (Cfr. Introduction, p. 43).

[17] Viene proposta anche una suddivisione delle disgiunzioni in due parti, ma di essa poi non si tiene conto nella numerazione dei gradi della scala universale.
[18] A. Daniélou, Traité de musicologie comparé, Herman, Parigi 1959, p. 59. (Abbr. Musicologie). Questo libro è in realtà un rimaneggiamento di Introduction.
[19] Introduction, pp. 229, 153.
[20] Musicologie, pp. 59, 60, 166. A p. 172 si parla anche di «divisione proporzionale dell’ottava».
[21] Talora Daniélou usa il termine di «armonia» (harmonie) per indicare «les rapports agréables des sons», Sémantique Musicale, Essai de psychophysiologie auditive, Hermann, Paris 1967 (I ed.) e 1978 (II ed.) p. 24. Abbr. Sémantique. Le citazioni sono tratte dalla seconda edizione.

3. Scala ciclica e "scala universale"
Se ci arrestassimo a questo punto la fragilità di questa costruzione sarebbe piuttosto evidente. Di fatto tutto si sostiene sulla pretesa «naturalità» degli intervalli primitivi e differenziali e sulla scala scala-tipo sulla quale essi vengono riportati. Questa pretesa è fondata fino a questo punto unicamente sul dato di fatto del loro impiego nella pratica musicale e sulla loro ipotizzata presenza in linguaggi musicali appartenenti a culture differenti (anche se si può effettuare questa costruzione senza allontanarsi di un passo dalla vecchia Europa). Ora non c’è dubbio che questo fondamento sia piuttosto fragile e non spiega a sufficienza in che senso debba essere inteso il riferimento alla «naturalità» o, se vogliamo, alla «naturalezza». Abbiamo dunque bisogno di qualche rafforzamento. A questo punto il discorso cade sul ciclo delle quinte che, come abbiamo già osservato, assume un ruolo importantissimo nell’impostazione di Daniélou, benché non prioritario.
Questo modo di «produzione delle note» e quindi di partizione dell’ottava si avvale degli intervalli consonantici fondamentali di quinta, quarta e ottava ed è quindi strettamente connesso con fatti uditivi concreti. Al tempo stesso esso può essere considerato anche come una sorta di algoritmo che può essere messo in movimento ben al di là delle esigenze della pratica musicale. Esso consiste a) nella iterazione successiva dell’intervallo di quinta realizzando ogni volta, se necessario, b) la riduzione all’interno dell’ottava che si intende suddividere [22] . Ciò che rappresenta il problema di questo metodo di partizione sta nel fatto che, per quanto ci si inoltri nell’iterazione, non si otterrà mai un valore coincidente con l’ottava - questo per ragioni puramente matematiche. E nemmeno si otterrà un valore coincidente con un punto già acquisito: ciò significa che nell’iterazione e nella riduzione all’interno dell’ottava si realizzerà una partizione progressivamente più fine dell’ottava stessa.
Ed ecco ora la circostanza che colpisce Daniélou: se realizziamo 53 cicli di quinte ed operiamo la riduzione necessaria otteniamo un punto che si approssima moltissimo all’ottava. Quell’insignificante numero 53, che sembrava appunto ridursi ad un mero dato di fatto, a qualcosa che dovevamo accettare perché avevamo trovato che le partizioni erano appunto quelle - e che sembrava quindi un dato alquanto accidentale, tende ad assumere un significato più pregnante una volta che lo si incontra in una partizione ottenuta secondo un metodo del tutto diverso, e per giunta puramente matematico. E ciò non basta ancora: a questa prima circostanza singolare si aggiunge la circostanza, che può sembrare ancora più straordinaria, rappresentata dal fatto che le partizioni ottenute con questo metodo coincidono talvolta esattamente talvolta approssimativamente con le partizioni ottenute secondo il metodo precedente: la scala «ciclica» coincide dal più al meno con la scala «armonica».
Scala Ciclica espressa in Cents
23, 47, 70, 94, 114, 137, 161, 184, 204, 227, 251, 274, 298, 318, 341, 365, 388, 408, 431, 455, 478, 502, 522, 545, 568, 592, 612, 635, 659, 682, 702, 725, 749, 772, 796, 816, 839, 863, 886, 906, 929, 953, 976, 1000, 1020, 1043, 1066, 1090, 1110, 1133, 1157, 1180, 1204
Daniélou ripete più volte che gli intervalli realmente corretti sono quelli fissati nella scala armonica [23] , e che non vi è identità tra i gradi della scala armonica e i gradi ottenuti per iterazione della quinta nella scala ciclica. E tuttavia «questi rapporti sono così prossimi l’uno all’altro che è quasi impossibile distinguerli direttamente» e che «nella pratica musicale... la questione della differenziazione sorge raramente» [24]. Ma che importanza può avere questa relativa corrispondenza tra le due scale?
In realtà, noi che abbiamo guardato con un certo scetticismo già la scala «armonica», saremmo tentati non tanto di rispondere a questa domanda ma di smontarla, smontando le due circostanze che dovrebbero suscitare la nostra meraviglia. Tutto dipende infatti da che gioco vogliamo lasciare a quel dal più al meno. Fino a che punto - dopo tanti calcoli - intendiamo spingere le nostre tolleranze nei confronti delle misure delle grandezze intervallari? Come abbiamo detto, in Daniélou talora si fa valere come significativa una micidiale esattezza nella caratterizzazione degli intervalli, talora invece si mostra la massima tolleranza, la massima disponibilità ad effettuare arrotondamenti ogni volta che possano per qualche ragione tornare utili. Ed in questo passaggio per certi versi cruciale sembra proprio giunto il momento della massima tolleranza. Nel caso dell’intervallo determinato dalla 53a iterazione della quinta, la differenza per eccesso rispetto all’ottava è di 3,64 cents. Non siamo obbligati, ma siamo padroni di considerare questa differenza tanto piccola da poter ritenere che l’ottava sia praticamente raggiunta dall’iterazione della quinta - prima condizione essenziale per meravigliarci della «coincidenza» sul numero 53. Siamo anche padroni di tollerare discrepanze quasi per ogni grado, e in particolare su gradi «importanti». Ma se siamo disposti a passar sopra a simili differenze, allora potrebbe sembrare piuttosto ovvio e niente affatto straordinario che due divisioni dell’ottava relativamente equilibrate e abbastanza fini, ed anzi finissime come è quella prodotta da 53 parti, conducano a risultati che si possono considerare affini [25] . Tutta la questione perderebbe così di interesse. Né la prima né la seconda circostanza sono in grado di provocare in noi il benché minimo entusiasmo.
Ma le cose stanno molto diversamente per Daniélou. A partire dalla convinzione dell’esistenza di scale naturali, e quindi dell’esistenza di un fondamento assoluto per esse, questa (pretesa) coincidenza tra l’apriori - rappresentato dalla scala ciclica che genera la partizione «matematicamente» - e l’empiria rappresentata dalla scala armonica il cui fondamento sarebbe insito nella stessa pratica musicale, viene considerata di fondamentale importanza proprio perché apporta alla «scala armonica» quel rafforzamento di cui essa ha bisogno. Tutto il problema sembra qui fare un salto di qualità ed assumere la sua reale fisionomia: la scala armonica «garantisce» per così dire, dal punto di vista musicale l’astratto matematismo del ciclo delle quinte, facendo venire meno le remore rispetto alle derivazioni puramente matematiche; mentre la scala ciclica finisce con il prestare l’alone del proprio matematismo alla scala armonica.
Si consolida dunque il rapporto con il mondo del numero, che era già fortemente presente nella scala armonica che richiedeva essa stessa i nostri bravi calcoli. Questo consolidamento significa soprattutto in Daniélou la ripresa delle antiche tematiche filosofico-metafisiche che facevano del numero principio del reale, e della musica la manifestazione sul piano della sensibilità di questo principio. L’unità tra scala armonica e scala ciclica è da considerare come una manifestazione sul piano fenomenico dei «principi metafisici dei suoni», cioè di quei principi che riportano al nucleo più profondo della realtà stessa [26] . La posizione di Daniélou è esemplare per il fatto che si regredisce, in rapporto al problema di una fondazione oggettivistica, dal fisicalismo all’aritmetismo, compiendo in certo senso a ritroso il cammino che conduce dal punto di vista aritmetizzante che si era affermato a partire dalla cultura greca fino al tardo rinascimento ed oltre, alle fondazioni nella fisica del suono. Il punto di vista aritmetizzante tende a separare il numero dalla realtà corporea, e proprio per questo a considerare il numero in se stesso come principio del reale, aprendosi ad ogni sorta di speculazione filosofica sulle virtù dei numeri come tali. Quando invece il rapporto numerico viene attribuito alle vibrazioni di un corpo elastico ed avviene così la ricongiunzione del numero con l’elemento fisico, le considerazioni metafisiche regrediscono sullo sfondo, la numerologia interessa assai meno di quanto interessi una possibile analisi della costituzione interna del suono come evento della natura. E l’intero problema tende a particolarizzarsi, allentandosi i legami con i fenomeni non appartenenti alla musica che in precedenza potevano essere tenuti stretti con analogie numerologiche.
Ora, in Daniélou, la critica di una fondazione della scalarità negli armonici e quindi il rifiuto di un naturalismo a base fisicalistica, non comporta il rifiuto di una concezione naturalistica in genere, ma piuttosto lo spostamento dell’attenzione verso il versante della «natura umana», quindi verso un versante psico-fisiologico. In questo ambito vanno ricercate le giustificazioni ultime. Nello stesso tempo si torna a guarda con interesse ad una fondazione puramente «aritmetica» che riprende gli interessi metafisici di un tempo. Si ripresentano così le speculazioni numerologiche di sapore antico, in un vero e proprio soprassalto neopitagorico in pieno secolo ventesimo. C’è chi ha osservato che la passione numerologica non è una malattia, ma quasi [27] . E questo può essere vero. Eppure, di fronte ad affermazioni come queste è anche il caso di diffidare. La storia della scienza e dell’arte insegnano che non sempre il pensiero cammina con i piedi di piombo e che non è in generale vero che l’enfasi sulla «positività» spalanchi senz’altro le porte ad intelligenza e comprensione. La vicenda del pensiero ha le proprie complicazioni, e in particolare le ha la teoria della musica che è una straordinaria mistura di scienza, esperienza diretta, tecnica, riflessione e immaginazione. Attraverso stravaganze, ostinate idee fisse, giri traversi - se si ha la pazienza e, vorrei anche dire, l’umiltà di adeguarvisi provvisoriamente - si viene in chiaro sulle motivazioni che stanno alla loro base, e sono proprio queste motivazioni che meritano spesso di essere portate alla luce.
Note
[22] Dal punto di vista calcolistico, le operazioni da compiere sono dunque due: ragionando in cents, si somma 702 a partire da 0, e si detrae iterativamente 1200, se dalla somma risulta un numero superiore a 1200; ragionando in rapporti, si moltiplica iterativamente per 3/2 a partire da 1, e la riduzione all’interno dell’ottava si ottiene dividendo il risultato per 2, finché non si è raggiunto un valore compreso tra 1 e 2.
[23] Introduction, p. 237.
[24] ivi.
[25] È stato anche osservato che tanto varrebbe ricorrere ad una scala equalizzata di 53 gradi. Cfr. P. e U. Righini, Il suono, Milano 1974, p. 198.
[26] Introduction, p. 236.
[27] P. e U. Righini, op. cit., p. 197 - proprio a proposito della «scala universale» di Daniélou.

4. Digressione neopitagorica e la mente come calcolatore
Il tentativo di tenere insieme aritmetismo e naturalismo psico-fisiologico è realizzato da Daniélou soprattutto nella Semantica musicale. L’idea dell’essenza numerica del reale viene elaborata qui in primo luogo dal punto di vista soggettivo, cioè dal lato della ricezione e dell’elaborazione dei dati percettivi [28] . La forma numerica dà la sua impronta ai nostri processi mentali: questa idea che ha radici così antiche si incontra inaspettatamente - e vorremmo quasi dire nello stesso tempo genialmente e ingenuamente - con la «scienza del calcolatore», con la «cibernetica». Questo libro contiene in effetti una grande quantità di citazioni di Norbert Wiener e di altri autori dello stesso ambito. Di qui deriva l’idea principale, sulla quale ha lavorato la psicologia cognitiva, secondo la quale il calcolatore può rappresentare una sorta di modello per lo studio dei processi mentali: «Il nostro apparato mentale funziona come una macchina da calcolo...» [29]- Daniélou ripete più volte; ma derivano di qui anche le idee-guida che gli consentono di fornire un’impostazione della propria problematica in un quadro di insieme. In particolare l’idea che nella mente (memoria) vi siano delle «figure-tipo» (patterns) e che la percezione consti di continui «ritorni» (feedbacks) ad esse come norme a cui confrontare il materiale percepito [30] . Ecco allora che, per quanto riguarda il nostro problema, gli intervalli percepiti sono costantemente riportati a modelli interni e viene sempre effettuato il tentativo di farli coincidere con essi, cosa che costa più o meno sforzo a seconda della prossimità o della distanza degli intervalli uditi rispetto ai modelli. Qui si risente aria di platonismo. Le figure-tipo sono in effetti come le idee di Platone a cui i materiali empirici vengono commisurati e interpretati. Attraverso un cerchio impreciso della percezione intravediamo il cerchio ideale di cui parla la geometria.
Ma come sono costituiti questi intervalli ideali che fungono da modelli? Il richiamo al calcolatore serve a Daniélou per dar corpo a qualcosa di simile ad una teoria. Ciò da cui egli è colpito è il fatto che i calcoli effettuati dal calcolatore, sono fondati su un sistema numerico peculiare che, in luogo di essere, come quello che utilizziamo correntemente, a base dieci è a base due. Naturalmente la base, in questo caso, non è indifferente al funzionamento del calcolatore, ovvero c’è una relazione tra il modo in cui il calcolatore «pensa» e il sistema numerico a base binaria. Ora proprio questa relazione interessa a Daniélou: la «mente musicale» - che va concepita come parte di un «calcolatore» certamente molto più complesso delle nostre macchine - funzionerebbe a sua volta su tre sistemi numerici, precisamente a base 2, 3 e 5 [31] . «Sembra che il nostro meccanismo mentale funzioni come una macchina calcolatrice che combini circuiti che lavorano in binario, ternario e quinario. Questa sembra essere la sola spiegazione, applicabile in tutti i casi conosciuti, dell’importanza di certi intervalli, del valore relativo di altri e dell’esclusione di alcuni, nei diversi sistemi musicali» [32]. È inutile dire che né il calcolatore né i sistemi numerici sono responsabili dei discorsi che di qui in avanti vengono sviluppati dal nostro autore. Dal punto di vista musicale questi tre numeri ci riportano naturalmente all’ottava, alla quinta ed alla terza - e propongono in generale un ritorno alla tematica della semplicità dei rapporti come sinonimo di naturalità e perfezione. Ciò potrebbe sembrare strano per il fatto che, sia nella formazione della scala armonica che in quella della scala ciclica sono presenti rapporti tutt’altro che semplici e persino vertiginosi dal punto di vista delle grandezze numeriche interessate: ma viene qui avanzata l’idea della possibilità di riportare tutti i rapporti validi della «scala universale dei suoni» («scala armonica») proprio a queste radici elementarissime dei primi tre numeri primi - argomento che riprenderemo tra poco. Inoltre essi sarebbero portatori, secondo Daniélou, di classi (o tipologie) affettive che avrebbero poi il loro puntuale riscontro nell’intervallistica musicale. Per convincerci di ciò, Daniélou fa spesso riferimento, nel più classico stile pitagorico, a rappresentazioni figurative dei numeri, a qualcosa di simile al loro corrispondente visivo-figurale: rappresentazioni che dovranno essere colte con l’occhio dell’immaginazione, naturalmente, anche se su questa partecipazione determinante della facoltà immaginativa non si potrà troppo calcare la mano per evitare una svalutazione dell’intera questione. Dunque, il 2 sarà rappresentativo della staticità, di un’idea di spazialità per così dire solidamente impostata e riposante su se stessa: naturalmente si può ben pensare a figure quadrate o rettangolari. Il 3 sarà invece rappresentativo di dinamismo e di movimento - e penseremo in tal caso a figure triangolari, mentre il 5 sarà rappresentativo della crescita organica, del momento vitale ed affettivo [33] . Per l’idea della crescita come incremento e sviluppo, Daniélou riesce a proporre con il pentagono un’analogia, sarei tentato di dire, quasi persuasiva [34] . Egli cita il problema della tassellatura di una superficie con figure geometriche. Mentre è possibile operare una tassellatura con rettangoli o triangoli senza variazione di grandezza, con il pentagono ciò è possibile solo ampliandone sempre più le proporzioni, come è mostrato dalla seguente figura [35] :

La crescita e lo sviluppo sembra dunque ben rappresentata dal punto di vista immaginativo. La vita emozionale è poi parte della vita stessa cosicché il cinque conterrebbe anche di essa il segreto. L’idea che ad un intervallo sia associato un «senso» e che questa associazione riguardi il numero che sta alla base del rapporto è continuamente ribadita in modi spesso sconcertanti. Dalla combinazione (prodotto) delle tre basi numeriche sorgerebbero intervalli «significativi», ovvero caratterizzati da una tonalità affettiva «mista» dipendente dalla combinazione considerata. Ad es. il 10, quando interviene nella determinazione di un rapporto intervallare, avrà carattere spaziale-emotivo essendo inteso come prodotto di 2 e 5, il 6 spaziale-dinamico (2*3), il 15 dinamico-emotivo (3*5) [36]. Il problema delle possibili valenze affettive è così ricondotto ad una questione di pura contabilità. Di una sconfinata ingenuità filosofica è poi il tentativo di trovare particolari significatività degli intervalli quando i numeri che costituiscono i loro rapporti siano riscritti nella notazione binaria, ternaria o quinaria [37] .
Ma a parte queste belle fantasie, vi è una circostanza che ci colpisce. Daniélou non accenna nemmeno alla possibile derivazione delle tipologie generali che egli propone per i primi tre numeri primi da circostanze di ordine musicale. In fin dei conti avremmo qualche buona ragione di ritenere che l’intervallo di ottava sia, come l’unisono, piuttosto statica. E non ci trova impreparati nemmeno l’idea che la quinta abbia carattere dinamico - così certamente questo intervallo è stato assai spesso usato! Quanto al fatto di attribuire valore emozionale al 5, si tratta - vedi caso - del numero caratteristico dell’intervallo di terza, sia maggiore (5/4) che minore (6/5): e la presenza dell’uno o dell’altro nell’impalcatura scalare determina una coloritura di variazione emotiva molto forte. A ben vedere si tratta di luoghi comuni del linguaggio musicale di tradizione europea - mi sembra il caso di sottolineare questo punto: ma si tratta di un punto che deve rimanere ben nascosto per il fatto che l’intero problema si capovolgerebbe, suggerendo che simili tipologie siano semmai proposte dal materiale musicale, ed anzi da un particolare linguaggio musicale, e proiettate sul numero, mentre per Daniélou le cose stanno esattamente all’opposto. Cosicché le analogie con le figure geometriche, facendo riferimento ad un materiale eterogeneo rispetto a quello musicale, sono certamente più produttive ai fini di quell’aggancio alla generalità che fa parte da sempre delle fondazioni aritmetiche della musica.
Note
[28] «Per la musica gli elementi che sono la sorgente delle sensazioni di piacere non possono che essere di natura numerica poiché noi non percepiamo altro che dei rapporti di frequenza, dei rapporti di tempo, dei rapporti di intensità e combinazioni di questi rapporti.», ivi, p. 24.
[29] ivi, p. 15.
[30] «I meccanismi con i quali noi critichiamo e valutiamo le nostre percezione utilizzano sia elementi nuovi della percezione, sia degli elementi già classificati. Il principale apparato critico del nostro cervello è ciò che si chiama meccanismo di feedback" ivi, p. 18. "Quasi tutti i nostri gesti sono regolati da feedback. Quando vogliamo prendere un oggetto, la precisione del nostro gesto dipende da un impulso regolato da una serie di feedback. Quando a seguito di danni in certe parti del cervello il meccanismo di feedback si inceppa il nostro gesto va troppo a destra o troppo a sinistra ...» . ivi, p. 19.
[31] I numeri 2, 3 e 5 come fondamento della suddivisione dell’ottava hanno una loro storia nella teoria della musica, basti rammentare Eulero (cfr. Patrice Bailhache, Une histoire de l’acoustique musicale, CNRS Ed., Paris 2001). Eulero a sua volta cita da una lettera di Leibniz: "Nella musica non sappiamo contare al di là di cinque, simili in questo a quei popoli che non vanno oltre il numero tre e che sono all’origine del detto tedesco sull’uomo semplice: ‘Non sa contare al di là di tre’ "(ivi, p. 125). Del resto anche Descartes osserva, nel suo Compendium Musicae: «advertendum est tres esse dumtaxat numeros sonoros, 2, 3 et 5, numerus enim 4 et numerus 6 ex illis componuntur, atque ideo tantum per accidens numeri sunt sonori...» (cfr. trad. it. Breviario di musica, Passigli, Firenze 1990, p. 87).
[32] ivi, p. 24.
[33] «Il numero 5 ‘umanizza’ la musica. Esso la rende strumento dell’espressione non più di astratti prototipi ma di una realtà tangibile" (Introduction, p. 231). "Il fattore cinque è il fattore più importante nella musica perché è esso che serve nel nostro meccanismo mentale ad esprimere la sensazione, l’emozione, il sentimento» (Sémantique, p. 46).
[34] ivi, p. 47.
[35] R. Penrose, La mente nuova dell’imperatore, Rizzoli, Milano 1992, p. 180: «Ci chiediamo se sia possibile ricoprire completamente il piano, senza vuoti e senza sovrapposizioni, usando solo queste forme e non altre. Una tale disposizione di forme è chiamata tassellatura del piano. Sappiamo bene che tali tassellature sono possibili usando solo quadrati o solo triangoli equilateri, o solo esagoni regolari, ma non usando pentagoni regolari».
[36] Sémantique, ivi, p. 49.
[37] ivi, p. 53.

5. La derivazione calcolistica della scala universale
A partire da questo impianto, possiamo ora tornare sui nostri passi per rendere conto dell’ultimo importante sviluppo che abbiamo annunciato poco fa. In realtà avremmo dovuto forse riferire su di esso fin dall’inizio, in rapporto all’introduzione della «scala armonica». Infatti, mentre noi abbiamo illustrato il percorso che conduce ad essa passando attraverso la partizione degli intervalli che abbiamo chiamato primitivi, sia nell’Introduzione, sia nella Musicologia comparata sia infine nella Semantica musicale si presenta un modo di accesso essenzialmente differente che manifesta un clamoroso ritorno alla «teoria dei rapporti semplici», forzando al massimo il legame con le considerazioni aritmetico-numerologiche nello spirito delle premesse di ordine generale che abbiamo illustrato or ora. Ciò che si tenta di fare è una derivazione dei gradi della scala armonica che è in realtà riportabile ad un modello puramente calcolistico, anche se Daniélou preferisce tenere questa circostanza alquanto nascosta, proponendo una descrizione dei passi da compiere per giungere al risultato e questo stesso risultato sotto la forma di una tabella descrittiva, piuttosto che metterci senz’altro sott’occhio un algoritmo come sua origine. Come abbiamo detto in precedenza, in questa nostra esposizione abbiamo seguito un percorso tutto nostro nel tentativo di mettere ordine nella trattazione di Daniélou, sostanzialmente priva di indicazioni metodiche ed in realtà niente affatto perspicua. Attraverso questo nostro riordinamento forse si riescono a fare emergere i fili conduttori interni così come elementi per una critica che non si contenti - come spesso è accaduto - di attaccare aspetti vistosi, ma di superficie, senza arrivare nemmeno a percepire il senso complessivo dell’operazione compiuta.
Ci accingiamo così ad illustrare quella che potremmo chiamare la seconda via di accesso alla scala universale dei suoni. Essa ha come scopo di dare la massima evidenza al dominio dei tre numeri fondamentali - 2, 3, 5 - sull’intero mondo sonoro-musicale; e vi è forse modo migliore di raggiungere questo scopo che quello di mostrare che dall’impiego di questi soli tre numeri si può rendere conto di tutti gli intervalli della scala armonica? «Rendere conto» non può qui che voler dire: mostrare che tutti questi intervalli sono derivabili, nella loro esatta determinazione, a partire da una formula che contiene unicamente questi tre numeri. Impresa apparentemente disperata! Eppure...
L’idea che sta alla base di tutta la costruzione è quella di un utilizzo, per così dire, accorto del ciclo delle quinte. Poiché si tratta di tentare una vera e propria derivazione calcolistica della scala, è naturale che si pensi ad un utilizzo del ciclo delle quinte, per via dell’automatismo che lo caratterizza. Sappiamo tuttavia già che questo utilizzo dà solo valori approssimativamente simili a quelli della scala armonica. Tuttavia Daniélou nota che per i primi giri di quinte - e precisamente per i primi quattro - si ottengono rapporti sostanzialmente coincidenti con i rapporti «armonici» [38]. Si tratta allora di realizzare dei segmenti di cicli delle quinte, ciascuno che prenda le mosse da un inizio differente, ottenendo così delle «serie» di intervalli. Ogni serie sarà costituita mediante quattro quinte ascendenti e quattro quinte discendenti, ciascuna ridotta entro l’ottava, e consterà quindi di otto intervalli. Gli elementi della serie saranno di conseguenza nove. Sola eccezione è rappresentata dalla cosiddetta Serie di base in rapporto alla quale Daniélou ritiene di dover utilizzare cinque cicli di quinte sia in direzione ascendente che discendente. Si otterranno dunque undici elementi. Precisamente Daniélou propone di generare sette serie, che verranno poi combinate insieme riordinando gli elementi in ordine crescente. Il risultato finale sarà una successione di intervalli sovrabbondante rispetto ai 53 intervalli della scala armonica. Questa lista andrà dunque depurata dagli intervalli eccedenti - mentre il punto essenziale è che essa contiene tutti i 53 intervalli, e questa volta secondo rapporti esatti.
Per scendere appena in qualche dettaglio necessario per comprendere meglio la procedura adottata: anzitutto produrremo una serie che chiameremo serie di base con inizio nella «tonica» - cioè nella nota di base. Poiché si tratta di determinare una scala relativa di intervalli, possiamo dare valore 1 a questo inizio ed assumerlo come do. Si otterrà la serie di base realizzando, come abbiamo detto or ora, cinque cicli di quinte sia nella direzione discendente che in quella ascendente [39] .
Si scelgono poi due nuovi rapporti come inizi e precisamente il rapporto di 6/5 (terza minore, 316 cents) e di 5/3 (sesta maggiore, 884 cents). La ragione di questa scelta, spiega Daniélou, è che si tratta dei rapporti più semplici in cui il numero cinque appare al denominatore ed al numeratore. Così sia. Ciascuno di questi due numeri può essere elevato alla seconda ed alla terza potenza generando ciascuno due nuovi rapporti, ciascuno dei quali verrà considerato come primo elemento da cui dare origine ad una nuova serie. Di conseguenza abbiamo tre serie che hanno alla loro base l’intervallo 6/5 (e che vengono chiamate da Daniélou Serie +, Serie ++, Serie +++ ) i cui inizi saranno rispettivamente 6/5, 36/25 e 216/125) e tre serie che hanno alla loro base l’intervallo 5/3 (e che vengono chiamate da Daniélou Serie -, Serie - - , Serie - - - ), i cui inizi saranno rispettivamente 5/3, 25/9 e 125/27, questi due ultimi riportati, nella riduzione entro l’ottava, a 25/18 e 125/108. Ciascuna serie verrà generata nello stesso modo descritto sopra per la serie di base, ma con solo quattro cicli di quinte. Non sorprenderà, date le considerazioni precedenti sul rapporto tra numeri ed espressività, che a parere di Daniélou, «tutte le note di una serie corrispondono ad uno stesso genere di espressione, mentre ciascuna delle serie corrispondenti a tipi di espressione differenti. Queste serie possono dunque essere chiamate ’categorie d’espressione’ (shruti-jati-s)» [40]. Questa affermazione è interessante, non tanto per l’allusione al concetto indiano di una connotazione affettivo-emotiva delle strutture scalari, che è troppo generico per avere particolare significato, quanto per il fatto che essa mostra che queste sette serie sono, nelle intenzioni di Daniélou, qualcosa di simile a dei «modi». È possibile che la dizione di «scala modale» per la scala universale dei suoni derivi proprio da questo spunto - cioè dal fatto che essa poggerebbe su sette sequenze assimilabili a modi.

In questo grafico sono riportate le sette serie, considerando quattro cicli di quinte. I valori sono ridotti entro l’ottava e riordinati scalarmente. Daniélou intende tuttavia acquisire nella scala il rapporto 243/128 e il rapporto 256/243 (limma pitagorico), pur ritenendolo equivalente a 135/128, ed entrambi si possono ottenere solo con un quinto ciclo di quinte sulla serie di base che presenta dunque due valori in più. Le caselle barrate contengono i valori non considerati da Daniélou perché ritenuti non utilizzati nella pratica musicale: debbono perciò essere «spuntati» [41]. Per pervenire alla scala universale, si tratterà soltanto di associare in una unica lista tutti i valori dei rapporti ottenuti nelle sette serie riordinandoli in ordine di grandezza.
Scala universale generata mediante le sette serie
1, 81/80, 128/125, 25/24, 256/243, 16/15, 27/25, 800/729, 10/9, 9/8, 256/225, 144/125, 75/64, 32/27, 6/5, 243/200, 100/81, 5/4, 81/64, 32/25, 125/96, 320/243, 4/3, 27/20, 512/375, 25/18, 45/32, 64/45, 36/25, 375/256, 40/27, 3/2, 243/160, 192/125, 25/16, 128/81, 8/5, 81/50, 400/243, 5/3, 27/16, 128/75, 125/72, 225/128, 16/9, 9/5, 729/400, 50/27, 15/8, 243/128, 48/25, 125/64, 160/81
Conversione in Cents della scala universale [42]
0, 22, 41, 71, 90, 112, 133, 161, 182, 204, 223, 245, 275, 294, 316, 337, 365, 386, 408, 427, 457, 477, 498, 520, 539, 569, 590, 610, 631, 661, 680, 702, 723, 743, 773, 792, 814, 835, 863, 884, 906, 925, 955, 977, 996, 1018, 1039, 1067, 1088, 1110, 1129, 1159, 1179
Se si confronta questo risultato con quello ottenuto attraverso il metodo di partizione degli intervalli primitivi
Partizione ottenuta con la partizione degli intervalli primitivi
0,22, 41, 70, 90, 112, 134, 161, 182, 204, 226, 245, 274, 294, 316, 338, 365, 386, 408, 427, 456, 476, 498, 520, 539, 568, 588, 610, 632, 659, 680, 702, 724, 743, 772, 792, 814, 836, 863, 884, 906, 925, 954, 974, 996, 1018, 1045, 1066, 1088, 1110, 1129, 1158, 1178
si noterà che essi sono sostanzialmente equivalenti, essendo dovute le piccole discrepanze al diverso modo di approccio ed alle approssimazioni inevitabili della misura in cents. Unica eccezione il quarantesettesimo grado che presenta 1045 cents contro 1039. In effetti si tratta di due scelte egualmente possibili dal punto di vista calcolistico, dal momento che il primo intervallo corrisponde a 4000/2187 (ed appartiene alla Serie - - -) mentre il secondo corrisponde a 729/400 (ed appartiene alla serie + +).
Note
[38] Musicologie, p. 59: «Nella serie delle quinte gli intervalli al di là della quarta quinta (81/64) non sono musicalmente accettabili e tendono a confondersi con gli intervalli armonici vicini che corrispondono a relazioni più semplici».
[39] Per ottenere un ciclo in direzione discendente si opera la moltiplicazione iterata per 2/3 e si riporta il valore ottenuto all’interno dell’ottava come quarta ascendente mediante moltiplicazione per 2.
[40] Musicologie, p. 60.
[41] Il confronto va fatto con la Tav. IX, della Musicologie (p. 172 segg.), che rappresenta la sistemazione definitiva data da Daniélou alla questione. Inutile aggiungere che queste scelte non potranno mai essere realmente giustificate e sono destinate a restare del tutto arbitrarie. Si noti che la tabella di p. 62 è solo in parte depurata dei valori ritenuti non utilizzati, in parte contiene valori che poi non entrano nella scala universale.
[42] Nella Musicologie, p. 172, Daniélou propone anche le misure in cents operando un arrotondamento del comma a 20 cents e delle disgiunzioni a 32 cents. Purtroppo così facendo il tono piccolo diventa di 184 cents e la somma complessiva degli intervalli risulta essere 1204, anziché 1200....

6. La formula che sta alla base della scala universale
Giunti a questo punto ci si potrà chiedere se non sia possibile operare una semplificazione che riporti la costruzione dell’intera scala universale ad un’unica formula di calcolo. Questa possibilità è suggerita dal fatto che alla base di ciascuna delle sette serie vi sono formule strettamente affini tra loro.
La Serie di base può essere generata da
1.

Si assumerà che y possa variare tra -4 e +4, prendendo sia valori positivi che negativi. Rammentando che ogni numero con esponente 0 è, per convenzione, eguale a 1, per y=0 si otterrà il primo elemento della serie. I valori positivi di y produrranno le quattro quinte ascendenti, mentre i valori negativi le quattro quinte discendenti [43] .
Le tre serie prodotte a partire da 6/5 saranno generate dalla formula
2.

dove x varierà tra 1 e 3, per ottenere i tre valori iniziali di esse, essendo y =0, mentre per y che varia da 1 a 4 e da -1 a -4 si otterranno quattro quinte ascendenti per i valori positivi e quattro quinte discendenti per i valori negativi.
Le tre serie prodotte a partire da 5/3 saranno generate dalla formula seguente che ha ovviamente le stesse spiegazioni.
3.

Queste tre formule possono essere riunite in una sola. Risulta anzitutto chiaro che la seconda formulasi riduce alla prima per x = 0, e quindi la «contiene». Nel caso della terza formula occorre tener presente che 5/3 è eguale all’inverso di 6/5 moltiplicato per due. L’inversione di 6/5 si ottiene ipotizzando nella seconda formula un esponente x negativo e integrando in essa una variabile z che ha la sola funzione di introdurre un moltiplicatore 2 nel caso in cui x abbia valore negativo. Di conseguenza la formula seguente [44] :
4.

può sostituire le tre formule precedenti. In essa, come abbiamo spiegato, x potrà variare tra -3 e +3, y tra -4 e +4 (oppure tra -5 e +5 volendo ottenere cinque cicli di quinte), z tra 1 e 2 essendo posta la condizione che z = 1 se x è positivo o pari a 0, altrimenti z = 2. Dunque x positivo è rappresentativo delle serie «+», x negativo delle serie«-», x =0 della serie fondamentale; mentre y positivo è rappresentativo delle quinte ascendenti e y negativo delle quinte discendenti, y=0 del primo elemento di ciascuna serie. Si intende che tutti i valori prodotti, se necessario, dovranno essere ridotti entro l’ottava, e le serie ottenute andranno unificate e riordinate in ordine di grandezza. Ma non basta: la formula 4. può essere sottoposta ad una trasformazione algebrica, che è assai meno trasparente di essa, ma illustra a meraviglia il tema della riduzione di tutti gli intervalli musicalmente validi (secondo Daniélou) ai numeri 2, 3 e 5. Questa formula può essere considerata finalmente il nostro punto di approdo:
5.

Attribuendo correttamente i valori delle variabili x, y, z si possono ottenere tutti i cinquantatré rapporti della scala universale di Daniélou [45] .
Anche se nella nostra esposizione abbiamo fatto il possibile per portare di passo in passo a questo esito conclusivo, esso probabilmente apparirà in ogni caso sorprendente. Se la «scala universale dei suoni» è in qualche modo una superscala, questa formula è certamente una superformula. Essa dovrebbe celare il segreto della divisione perfetta dello spazio sonoro e formare il quadro di riferimento per giudicare intorno alla perfezione di ogni scala possibile. Il punto che mi sembra anzitutto di dover sottolineare è che la «teoria dei rapporti semplici», giocata ora sui tre più piccoli numeri primi, si separa nettamente dalla nozione di consonanza a cui in realtà quella teoria è per lo più stata legata - e ciò è particolarmente significativo, dal momento che il vincolo di quella teoria agli intervalli consonanti fondamentali rappresenta un vincolo al piano della percezione. Operando questa separazione questo legame viene semplicemente tolto. L’idea delle «virtù» musicali dei numeri come tali riceve qui la sua massima esaltazione. Con particolare chiarezza si insegna poi che la semplicità non è da ricercare tanto nei rapporti numerici che caratterizzano gli intervalli come tali (che sono per lo più tutt’altro che semplici) ma nelle loro radici esibite dalla formula con cui possono essere costruiti. In quella superformula compaiono esclusivamente i numeri 2, 3, e 5 come costituenti la base dell’intervallistica musicale in generale. Non può sfuggire infine in che misura in quella formula il ciclo delle quinte venga nuovamente celebrato. L’intera produzione degli intervalli «possibili» è affidata al ciclo delle quinte - essendo sempre il moltiplicatore 3/2 che determina gli elementi di ciascuna serie.
Alla luce di ciò appare assai singolare che questa superformula non venga apertamente esibita, ed anzi posta in apertura di tutto il discorso sulla scala universale, ma venga soltanto lasciata trasparire e suggerita tra le righe. È il lettore attento che deve rendersi conto della sua presenza. In luogo di questa enorme semplificazione formale, Daniélou preferisce ricorrere a descrizioni verbali della procedura affidandosi a tabelle e grafici non sempre di facile decifrazione. Nel grafico seguente si cerca di dare rappresentazione all’intero sistema delle sette serie, ai loro valori intervallari, con una puntigliosa ripresa dei nomi delle note che vengono differenziati secondo la loro appartenenza a ciascuna serie.
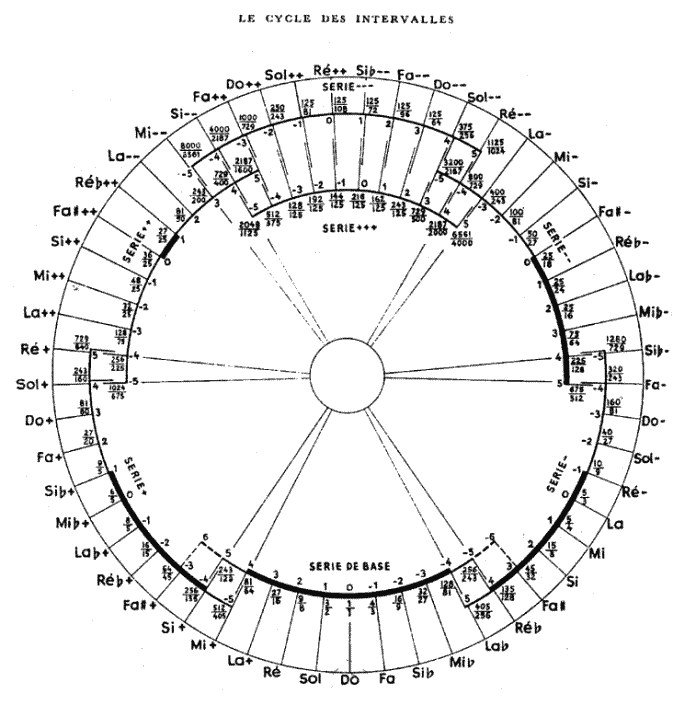
Ma si tratta solo di un esempio. Tabelle e grafici abbondano dappertutto. Tutto viene considerato per così dire nota per nota, intervallo per intervallo. Nulla dunque di più distante dalla sinteticità della nostra piccola formula - di cui il lettore non viene da nessuna parte chiaramente informato. Io credo che di tutto ciò vi sia una ragione tutta interna all’impostazione proposta. Come abbiamo notato fin dall’inizio Daniélou vuole attenersi il più possibile alla concretezza dell’esperienza musicale. Egli è stato indubbiamente un grande «osservatore» e «misuratore» di intervalli - a lui spettano meriti importanti per quanto riguarda la necessità da parte della musicologia di rispettare le grandezze intervallari realmente utilizzate da altre civiltà musicali [46] . Ma il modo in cui imposta il problema di una fondazione oggettiva della divisione dell’ottava, oltre che, naturalmente, lo sfondo filosofico generale entro cui si muove, lo spingono in direzione di una forte ripresa della tradizione matematizzante e nel risultato finale, in cui vediamo i cinquantatré gradi della sua «scala universale» per così dire emessi da un giocattolo meccanico, la concretezza dell’esperienza musicale rischia di essere spazzata via. Sorge il dubbio che proprio di essa si sia tenuto conto solo in apparenza, che fin dall’inizio, essa sia stata irregimentata in modo da adeguarla a questi esiti. Un equilibrio tra questi due momenti non può certo essere facilmente mantenuto. Meglio dunque un grande tabella da cui si intravveda appena la possibilità di una formula generale, piuttosto che una formula generale messa in prima pagina che toglie in un colpo solo la necessità di una tabella. Mettiamo un po’ in ombra la formula generale per evitare che questa schiacci le nostre intenzioni di attenerci in prossimità dell’esperienza musicale e le renda in certo senso improbabili. D’altra parte questa esperienza finisce con il non essere altro che il rispecchiamento della struttura matematica necessaria della realtà e della struttura della nostra mente. Cosicché alla fine, al di là delle oscillazioni che sono un ulteriore sintomo di incertezza metodica in cui si muove l’intera impostazione, non ci si può esimere dall’assumersi l’intera responsabilità della formula generale, che rappresenta il pilastro effettivo che sostiene tutta questa costruzione.
Il percorso che abbiamo descritto può essere considerato esemplare proprio per il fatto che presenta una forma estrema di fondazione metafisico-aritmetica della musica riprendendo un’istanza teorica che sembrava definitivamente superata dal prevalere delle fondazioni a orientamento fisicalistico. Elementi per una critica sono presenti dappertutto nella nostra esposizione - e sono elementi che non si contentano di una levata di spalle, come si potrebbe anche fare rispetto alle prese di posizioni più squilibrate di Daniélou. Volendo riportarli ad un unico punto focale, credo si debba attirare l’attenzione soprattutto sul modo di atteggiarsi nei confronti dell’ottava come spazio sonoro e naturalmente sul modo di concepire l’intervallo. L’ottava viene considerata come se avesse già in sé un numero determinato di comparti. Essa consta semplicemente di intervalli più grandi costituiti da intervalli più piccoli. L’ottava non è altro che una punteggiatura di intervalli, una sorta di asse sul quale debbono essere sistemati dei chiodi. Ciò che si deve scoprire è soltanto il luogo esatto in cui deve essere alzato il martello. Il punto di vista del «discreto» è ovunque dominante; e nonostante il gioco delle tolleranze che il buon senso musicale suggerisce, non è possibile fare a meno di avanzare ovunque un’esigenza di estrema esattezza. L’intervallo viene considerato qualificato dal rapporto numerico - e questo deve individuare una posizione assolutamente determinata. Ciò è richiesto dalla «razionalità» del rapporto. In via di principio si insiste perciò su determinazioni esatte - ed alle differenze impercettibili si affida spesso un differente valore semantico [47] ; nello stesso tempo dall’esattezza di quelle determinazioni si è sempre pronti a recedere quando vi sia un qualche motivo per non insistervi troppo. In rapporto all’attribuzione di significati emotivi particolari agli intervalli, risulta con particolare chiarezza la separazione dell’intervallo dallo spazio sonoro. L’intervallo viene preso in se stesso, indipendentemente dalla sua integrazione in uno «spazio» indipendentemente dal profilo fenomenologico che gli può essere attribuito in forza di questa integrazione; e si pretende che esso abbia un significato unicamente in base al rapporto che lo determina e quindi al fattore numerico che lo caratterizza.
Il considerare l’intervallo come qualificato dal rapporto numerico significa effettuare il passaggio ad un livello transfenomenologico. L’aritmetica deve sostituirsi alla fenomenologia. L’aritmetica interviene come calcolo delle posizioni, la numerologia provvederà nella misura del possibile a stabilire le premesse del calcolo e nello stesso tempo a dar senso all’insieme. Senza l’enfasi numerologica sul 2, 3 e 5, non avrebbe nemmeno senso il mettersi alla ricerca di formule. Nello stesso tempo senza una metafisica del numero non può esservi alcuna enfasi numerologica. Ne deriva una costruzione sistematica che sta tutta dentro questo cerchio e che piuttosto che richiedere di essere compresa, avanza la pretesa inaccettabile che vi si salti nel mezzo. Mi sembra infine che un risultato non secondario della nostra ricostruzione sia quello di aver mostrato quanto poco la posizione di Daniélou possa rappresentare un buon riferimento per una teoria delle strutture scalari di origine extraeuropea e quanto poco su di essa siano determinanti gli stimoli provenienti da tali tradizioni. Esito a dire una cosa simile per un autore come Daniélou, ma mi sembra proprio di doverlo dire.
Note
[43] Si rammenti che le quinte discendenti si otterranno iterando la moltiplicazione per 2/3 e che

[44] Uno spunto non elaborato per questa formula si trova nell’introduzione di F. Escal alla Sémantique, p. 8.
[45] I passi della trasformazione algebrica sono i seguenti:

[46]A questo proposito è il caso di segnalare che uno schema abbastanza simile a quello della derivazione delle sette serie di Daniélou è presente anche nello schema di accordatura del suo «clavier universel» che aveva lo scopo di «studiare tutti gli intervalli impiegati nei diversi sistemi musicali e per abituare l’orecchio ad intenderli». Cfr. Musicologie, App. III, pp. 176 sgg., e Sémantique, App. II, pp. 119 sgg.
[47] Può valere in proposito a titolo di esempio la differenza tra i due limma a 90 (256/243) e 92 (135/128) cents, che viene dichiarata sostanzialmente inavvertibile dal punto di vista uditivo. Ma nello stesso tempo si dichiara la differenza di significato funzionale tra i due intervalli, peraltro con motivazioni diverse, in Sémantique, p. 230 e in Musicologie, p. 169.

