Questo testo è stato pubblicato in De Musica, Internet, IV, 2000.
Data di immissione in questo archivio: Settembre 2000

![]() Giovanni Piana, La serie delle serie dodecafoniche e il triangolo di Sarngadeva (257.02 kB) (pp. 25)
Giovanni Piana, La serie delle serie dodecafoniche e il triangolo di Sarngadeva (257.02 kB) (pp. 25)
La lettura cosmologica del triangolo di Sarngadeva di Giovanni Ferrero
La serie delle serie dodecafoniche e il triangolo di Sarngadeva
 |
|
1. Che cosa è il "triangolo" di Sarngadeva
Nel trattato intitolato Oceano della musica (Sangitaratnakara) [1] uno dei più importanti testi classici della tradizione teorico-musicale indiana, Sarngadeva propone un’interessante digressione matematica sulla quale ci vogliamo anzitutto soffermare[2].
Nella sezione quarta del capitolo primo [3] Sarngadeva si propone di raccogliere in un’unità tutte le permutazioni possibili delle sette note della scala sagrama illustrando anche un metodo pratico per il loro completo dominio. Precisamente si tratta di realizzare una duplice operazione: da un lato, ad ogni permutazione deve poter essere associato un numero, dall’altro deve essere possibile «estrarre» da un determinato numero - ovviamente compreso tra 1 e il numero massimo di permutazioni possibili - la permutazione ad esso associata.
Volendo dare una idea della procedura proposta, faremo riferimento alla terminologia delle sette note della scala Sagrama i cui nomi sono:
Sa Ri Ga Ma Pa Da Ni
La grandezza degli intervalli è del tutto priva di importanza per il nostro problema, e da essa possiamo quindi prescindere. Data dunque una qualunque «variante» di queste sette note, ad esempio:
Ma Pa Ri Ga Sa Ni Da
dobbiamo essere in grado di assegnare ad essa un numero. E dovrà essere poi possibile «espandere» questo numero in quella «variante» .
Per indicare la direzione che procede dalla serie di note al numero Sarngadeva parla di una via o problema uddista[4] e di una via o problema nasta [5] per indicare la direzione inversa, dal numero alla serie.
Lo schema teorico che sta alla base della soluzione di questi problemi non viene dichiarata, mentre ci viene insegnato un metodo pratico che conduce direttamente e semplicemente al risultato voluto, come una sorta di gioco da realizzarsi con dei gettoni da disporre e da muovere su una apposita scacchiera numerica.
La scacchiera altro non è che una matrice numerica triangolare - ciò che noi vogliamo chiamare in breve «triangolo di Sarngadeva» . Il suo vero nome è Khandameru, che viene tradotto con «permutation-indicator» .
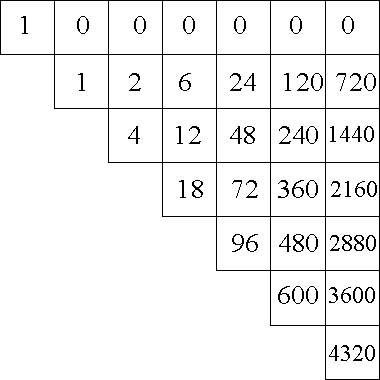
Nella prima riga, che è formata da sette caselle, la prima casella contiene 1 e tutte le altre 0. Le caselle della seconda riga sono riempite, nell’ordine, dai fattoriali dei numeri da 1 a 6. Tutte le altre righe sono riempite moltiplicando di volta in volta per 2, per 3, per 4, per 5 e per 6 il numero contenuto nelle caselle corrispondenti della seconda riga. Così il numero 4320 dell’ultima casella è 720 * 6.
Sul modo di «giocare» su questa scacchiera, a dire il vero, Sarngadeva offre indicazioni piuttosto criptiche e più che succinte[6]. D’altronde le spiegazioni che troviamo nel commento alla traduzione inglese sono, al contrario, anche troppo prolisse e non fanno facilmente intravvedere lo schema costruttivo di base. In realtà per venirne a capo senza troppe difficoltà, credo sia invece opportuno schematizzare la procedura pensando ad una sua possibile formalizzazione.
Sia Seq una sequenza di note e NumSeq il numero corrispondente. Il punto essenziale è che il passaggio nelle due direzioni tra Seq e NumSeq
Seq NumSeq
è mediato dalla formazione di due liste che chiameremo, usando una terminologia nostra, la lista degli indici di spostamento di posizione, sia S, e la lista dei costituenti del numero della sequenza, sia C.
Il processo uddista sarà dunque schematizzabile nel modo seguente:
Seq -> S -> C -> NumSeq
Il processo nasta invece:
NumSeq -> C -> S -> Seq
Tenendo presente questo schema potremo anche renderci facilmente conto del modo in cui si esegue il gioco con il «triangolo» . A questo scopo converrà prendersi qualche innocua libertà che renda ancora più agevole l’esecuzione. Sarngadeva suggerisce ad esempio di operare con dei gettoni o dei sassolini. Ma si potrebbe servirsi anche di anelli - che hanno il vantaggio di occupare le caselle della scacchiera lasciando visibile il numero che vi è scritto all’interno. I gettoni ci serveranno invece, una volta debitamente contrassegnati con i nomi delle note, per indicare la successione normale e le sue varianti combinatorie. Ne abbiamo dunque bisogno due serie di sette. Al di sopra della scacchiera triangolare, disporremo infine due righe di sette caselle che ospiteranno i nostri gettoni. Queste sono appunto alcune libertà che ci prendiamo.
La nostra scacchiera si presenterà nel modo seguente:

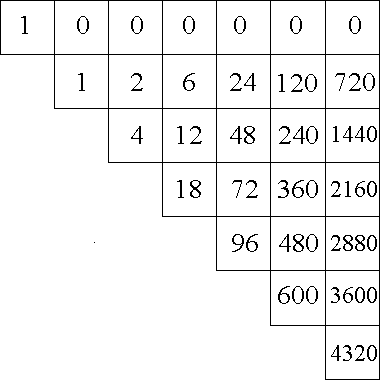
Nella riga superiore porremo i gettoni nell’ordine della forma normale della sequenza di note, a partire dalla quale sarà possibile identificare gli spostamenti intervenuti nel passaggio alla forma modificata, che verrà invece proposta nella riga inferiore.
Nella via uddista, il primo passo Seq->S, potrà essere realizzato operando sulle prime due righe.
Sia la forma normale
Sa Ri Ga Ma Pa Da Ni
e sia la forma modificata, a titolo di esempio:
Ri Sa Ma Ga Pa Da Ni
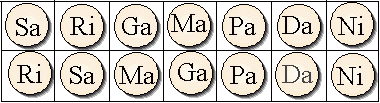
Per determinare la lista degli indici di spostamento si procederà prendendo in considerazione l’ultima sillaba delle forma modificata. Si conteranno i posti da destra a sinistra, includendo gli estremi, fino a raggiungere la stessa sillaba nella linea superiore, cancellando di volta in volta la sillaba raggiunta (ovvero: sopprimendo il gettone corrispondente). Il numero risultante dal conteggio rappresenterà un indice di spostamento di cui prenderemo nota a parte. Si sopprimerà poi il posto vuoto sulla riga superiore stringendo i gettoni sulla destra. Nel caso in cui non vi sia spostamento si attribuirà 1 come valore dell’indice di spostamento. Procedendo in questo modo sull’esempio si ottiene la seguente lista degli indici di spostamento di posizione
S = {1, 1, 1, 2, 1, 2, 1}
Questi numeri possono essere interpretati come indicatori di riga nella matrice triangolare: ad essi si può associare, da sinistra a destra, l’indicatore di colonna da 7 ad 1, ottenendo così coppie di numeri come indicatori di caselle.
1,7 1,6 1,5 2,4 1,3 2,2 1,1
Andando a leggere i valori contrassegnati nelle caselle corrispondenti da destra a sinistra otteniamo la sequenza di numeri
C = {0, 0, 0, 6, 0, 1, 1}
che abbiamo chiamato lista dei costituenti del numero della sequenza: in effetti il numero da assegnare alla sequenza modificata è pari al risultato della loro somma.
NumSeq = 8
Dal punto di vista del gioco con i gettoni e gli anelli, risulterà comodo fondere insieme i due processi.
Una volta ottenuto un certo indice di spostamento, ad es. 2, si scenderà di due passi sulla colonna della matrice triangolare che si trova sotto la lettera che è stata spostata e si porrà sulla casella così raggiunta un anello, con 1 si scenderà di un passo, ecc. Non vi sarà dunque bisogna di prendere nota degli indici di posizione perché questi vengono immediatamente utilizzati per identificare le caselle. Alla fine tutti i sette anelli saranno stati disposti sulle caselle dalle quali potranno essere letti i valori della lista dei costituenti.
La posizione iniziale prevederà dunque solo i gettoni nelle prime due righe. Nella posizione finale i gettoni saranno ancora presenti nella seconda riga presentando la forma modificata e gli anelli saranno stati distribuiti sulle caselle.
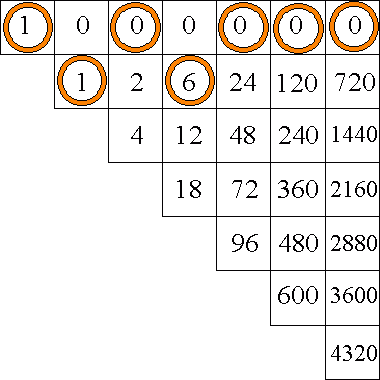
Nel caso della via nasta, dovremo a partire dal numero della sequenza (NumSeq) trovare anzitutto la lista dei suoi costituenti (C): poiché si assume che questa lista sia stata tratta da quella degli indici di spostamento si potrà riottenere quest’ultima (S), e di qui la forma permutata della sequenza di note (Seq) corrispondente a quel numero.
Converrà ora seguire una via direttamente esemplificativa.
Sia 18 il numero dato. Il primo passo consiste nel togliere 1 da 18. Otteniamo il numero 17. Ricorriamo ora alla matrice triangolare e cerchiamo in essa, procedendo da destra a sinistra, un numero minore di 17. Naturalmente potrebbero esservi vari numeri minori di 17. Noi prenderemo il maggiore di essi. Verrà considerato maggiore dei minori anche il numero stesso qualora venisse trovato nella matrice. Nella casella identificata in questo modo porremo uno dei nostri anelli. Occorre poi tener conto della seguente regola: ogni colonna eventualmente saltata dovrà essere contrassegnata con un anello disposto sulla casella corrispondente nella prima riga.
Nell’esempio, il maggiore dei minori di 17 risulta essere il 12, sul quale porremo uno dei nostri anelli. Poiché tuttavia le prime tre colonne sono state saltate, sugli zeri delle colonne corrispondenti nelle prime righe avremo posto tre anelli. Si farà poi la differenza tra 17 e 12 (ovvero tra il risultato dalla differenza precedente (18-1=17) e il numero trovato in tabella), ottenendo 5 e poi si procederà nello stesso modo cercando nella matrice il maggiore dei minori di 5. Verrà così contrassegnato con un anello la casella che contiene il numero 4, e poi operando nello stesso modo (5-4=1) porremo un anello sulla casella della seconda riga che contiene un 1. L’ultimo passo consisterà unicamente nell’occupare con un anello la prima casella della prima riga che contiene 1.
Abbiamo dunque contrassegnato con gli anelli sette caselle. Se andiamo a leggere i numeri nelle caselle contrassegnate dagli anelli otteniamo la sequenza C, che rappresenta una sorta di «analisi» di Numseq. Si tratta propriamente di
C = {0, 0, 0, 12, 4, 1, 1}
A questo punto il passaggio a S diventa semplice. Basterà raccogliere i numeri di riga in cui si trovano gli anelli. Questi numeri ci forniscono la lista degli indici di spostamento:
S ={1,1, 1, 3, 3, 2, 1}
Prendiamo ora i gettoni, e disponiamo la forma normale nella riga superiore. Procediamo su di essa considerandola a partire dall’ultima sillaba, mentre la lista degli indici verrà considerata da sinistra a destra. Alla sillaba Ni viene assegnato l’indice di posizione 1, cosicché non subirà alcuno spostamento e verrà trasferita nella riga inferiore. Analogamente per Da e Pa. Ogni volta si potrà per chiarezza stringere a destra i gettoni della riga superiore togliendo i vuoti. Trovando 3 come indice di posizione si conteranno tre posizioni da destra a sinistra nella riga superiore, si accosterà il gettone Ri ai tre gettoni già disposti sulla riga inferiore e così via. Alla fine si otterrà nella riga inferiore la forma modificata corrispondente al numero 18, ovvero
Ma Ga Sa Ri Pa Da Ni
Come nel caso precedente, giocando con i gettoni e gli anelli, si fonderanno i due momenti. Dopo aver disposto i gettoni nella forma normale nella riga superiore si opererà di passo in passo, prima disponendo l’anello e poi operando lo spostamento richiesto dal numero di riga, riportando di volta in volta il gettone dalla riga superiore a quella inferiore, secondo la procedura spiegata or ora.
Come abbiamo osservato, vi è qualcosa da guadagnare nel ripensare la procedura proposta da Sarngdeva nella prospettiva di una formalizzazione puramente calcolistica. Se poi realizzassimo questa formalizzazione, andremo naturalmente al di là di tutti i dettagli pratici relativi ad anelli ed a gettoni e avremo fra le mani niente altro che un calcolo, che nella sua versione informatizzata potrà fornirci i risultati in modo automatico. Si potrà allora vedere ancora meglio che la procedura Nasta, che fin qui abbiamo considerato come una sorta di «analisi» di un numero «rappresentativo» di un ordine da «estrarre» da esso, può invece essere intesa anche come una procedura di derivazione di tutte le permutazioni possibili di una lista di oggetti, nella quale ogni permutazione, come è necessario trattandosi di un calcolo, occupa una posizione esattamente determinata. Il numero d’ordine che una permutazione occupa in questa derivazione, e che quindi è in grado di identificarla univocamente, altro non è che ciò che abbiamo chiamato numero della sequenza.
Se ad esempio attraverso la procedura Nasta produciamo gli ordini da 1 a 24, per una serie di quattro oggetti - si potrà naturlamente ancora trattare delle prime quattro note della nostra scala - sa ri ga ma - otteniamo appunto una lista che è la lista di tutte le sue permutazioni possibili. La prima nell’ordine (Numseq=1) avrà come indici di spostamento {1,1,1,1}, mentre l’ultima {4,3,2,1}.
Alla base di tutta la questione vi è dunque l’idea di una successione ordinata di tutte le permutazioni possibili di una serie assunta come serie di base. E si può presentare il gioco con gettoni ed anelli sulla scacchiera triangolare come un modo per esplorarla [7].
L’intera questione sembra avere più un interesse matematico che musicale. Così almeno ad un primo sguardo. Anzitutto, come abbiamo notato, la successione di note che abbiamo chiamato «normale» , non riveste una particolare importanza, ed abbiamo ritenuto di non dover neppure accennare all’eventuale struttura intervallare vera e propria. In luogo della scala sagrama potremmo benissimo porre la nostra scala di do maggiore. Abbiamo abbiamo anche suggerito che in fondo potremmo pensare piuttosto che alle note, ai loro nomi. Persino il significato musicale di questi nomi potrebbe non interessarci e in ogni caso non incidere sull’intera questione. In effetti si tratta di un problema posto per una successione di oggetti in genere, dove ciò che importa è solo l’ordine iniziale di successione, la forma della successione, dunque, e non la natura degli oggetti posti in successione. La presenza di questo algoritmo nel trattato di Sarngadeva sembra possa essere genericamente giustificata al più richiamandosi all’interesse che la filosofia e la scienza indiana mostrano ovunque per questo genere di problemi.
Tuttavia io credo che occorra essere prudenti in questo genere di valutazioni. Nonostante la distanza che molto spesso la teoria musicale prende dalla pratica, vi è sempre una qualche dialettica interessante tra l’una e l’altra. La storia della musica è anche storia della teoria della musica, anche se si tratta di una circostanza che talvolta si tende a mettere molto in secondo piano.
Per quanto la questione posta da Sarngadeva non sia in se stessa specificamente musicale, forse in essa potremmo scorgere alcuni aspetti che sono volti al versante della musica. In realtà., io sarei tentato di vedere questo interesse matematico per la permutazione del tutto coerente con una forma mentis che agisce in profondità anche sul terreno dell’immaginazione musicale. Anzi: forse siamo qui in presenza di un bellissimo esempio di come pensiero astratto e pensiero concreto - ovvero quel pensiero che si muove nei pressi della percezione e dell’immaginazione - siano fusi l’uno nell’altro, anziché essere reciprocamente indifferenti o addirittura ostili.
A riflettere in questa direzione siamo stimolati da un bel libro scritto da Neill Sorrell in collaborazione con Ram Narayan - grande virtuoso del sarangi - intitolato Indian music in performance che si presenta, come dice il sottotitolo come A practical introduction[8].
In realtà, anche in questo caso, la pratica ha molto da insegnare alla riflessione teorica. Apprendiamo così per l’apprendimento della tecnica del sarangi il maestro indica all’allievo «esercizi molto semplici con le istruzioni per praticarli giornalmente per un anno o più» [9]. Questi piccoli esercizi vengono chiamati palta e sono caratterizzati dall’impiego di un numero ristretto di note con eventuali ripetizioni del tipo
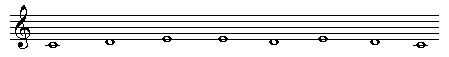
La pratica vera e propria consiste nella variazione - da vari punti di vista (velocità, accentazione, legature, trasposizioni) - del motivo del palta considerato. È allora subito chiaro che i palta nella loro forma più semplice, senza ripetizioni di note, altro non sono che le permutazioni di un numero dato di note [10]. Questo riferimento al sistema completo delle permutazioni viene qui esplicitamente rammentato, e si fa notare che si si aggiungono le possibilità di modificazioni ritmiche, se si ammettono ripetizioni, varietà nei raggruppamenti e nelle accentazioni, ecc. si possono ottenere variazioni di un numero elevatissimo da un piccolo gruppo di note, anche da sole quattro note - «probabilmente la lunghezza e la complessità ideale per un palta di di questo tipo» [11]. Tutte le ventiquattro permutazioni corrispondenti alle prime quattro note della scala vengono indicate come una sorta di sistema di riferimento di base.
La pratica con queste permutazioni consiste nella loro acquisizione completa attraverso l’esercizio, impiegandole anche nelle forme trasposte possibili nel registro dello strumento; quindi ciascuna permutazione viene modificata ammettendo la ripetizione di note appartenenti ad essa, ottenendo così elementi motivici un poco più ampi da riprendere anch’essi nelle loro trasposizioni.
Nell’esempio seguente, un palta di tredici note viene ripetuto undici volte in trasposizioni ascendenti e discendenti di un grado. Come appare da questo esempio il termine di trasposizione non deve essere preso troppo alla lettera.

Esempio di esecuzione:
Esso potrà poi essere eseguito secondo una varietà di accentazioni, di legature e velocità secondo l’inventiva, l’estro e l’abilità del musicista.
Esempio di esecuzione:
In entrambi gli esempi il brano è eseguito una quarta sopra.
I palta potranno poi entrare all’interno di un particolare raga, o connettersi ad esso in varie forme, ed in questo modo ci si comincia a staccare dalla tecnica elementare ed ancora musicalmente indifferente per entrare senza soluzioni di continuità in un’elaborazione propriamente musicale. Ed è proprio la possibilità di questo passaggio dalla pratica di apprendimento dello strumento all’opera musicale eseguita in concerto - dalla practice alla performance - che rappresenta un elemento particolarmente ricco di significato per il concetto della musicalità che si va in questo modo profilando[12]. Si prendono le mosse da schemi motivici in certo senso «meccanici» e già dati in anticipo, da cui si potrebbe escludere il sospetto di qualunque creatività e apparentemente preordinati unicamente all’acquisizione di una pratica strumentale - ma ci si rende conto che il modo in cui questa pratica viene esercitata introduce direttamente a quella che qui viene definita «the essence of Indian performance» - essenza che consiste nella «costante variazione e nell’estensione di ciò che può sembrare un materiale relativamente esiguo» [13]. È in questa costante variazione che cresce e si sviluppa la capacità improvvisativa - l’apparente meccanicità è messa qui al servizio di un dominio del materiale su cui deve contare la genialità e la creatività musicale. Scrive ancora Neil Sorrell: «Il padroneggiamento di questo genere di esercizio non solo migliora la tecnica, ma anche arricchisce il patrimonio di idee del musicista per l’improvvisazione, in quanto concentra la sua attenzione sull’abbondante potenzialità di un materiale tanto limitato... Non è un segreto per nessuno che la pratica di simili palta ha aiutato molti degli artisti più autorevoli a stabilire la loro fama come improvvisatori fluenti» [14].
Di qui possiamo anche trarre un’altra conseguenza interessante Proprio perché in ultima analisi è il musicista-interprete che prenderà ogni decisione, sulla base di strutture date, il pensiero che queste strutture siano in qualche modo precostituite, ed eventualmente addirittura pedantescamente numerate e distribuite in bell’ordine non disturba per nulla né il teorico né il musicista. Per il musicista si tratta infatti della delimitazione dello spazio entro cui si possono muovere le sue esplorazioni conoscitive e immaginative. Mentre il teorico potrà considerare come proprio compito precipuo il mettere ordine nell’esperienza musicale, operando classificazione e proponendo ordinamenti.
In Sarngadeva è presente in particolare - facendo riferimento esclusivo al Kandhameru che in realtà deve essere considerato un dettaglio minimo all’interno della sua grande opera - l’idea di una sinossi compiuta e completamente dominabile di tutto ciò che è possibile fare, almeno a livello intervallare, con un tipo melodico di base, che è appunto fornito dalla scala sagrama. Come abbiamo visto or ora, sarebbe un errore ritenere che a partire di qui nulla si veda sul versante musicale. Ma resta naturalmente vero che, per quanto riguarda la precisa delimitazione del problema, l’aspetto calcolistico è prevalente.
Ciò risulta chiaro se si confronta il Khandameru con altri progetti, di senso differente, in cui si fa tuttavia valere uno spirito sistematico altrettanto forte.
Penso, ad esempio, al progetto di sistemazione dei raga proposto da Venkatamakhin nel XVII secolo, con riferimento alla musica carnatica. In effetti è ancora una forma mentis matematico-combinatoria, una forma mentis «aprioristica» , che presiede a questa sistemazione, ma scopo e problema sono interamente diversi. Nel caso di Venkatamakhin si tratta soprattutto di portare ordine nella molteplicità indeterminata dei raga di fatto impiegati nella realtà musicale dell’epoca, cercando di individuare un ristretto numero di raga a titolo di raga «fondamentali» . Ciò avviene attraverso una schematizzazione teorica della struttura dell’ottava in base alla quale si determinano non più e non meno di settantadue raga, ciascuno dei quali riceverà un numero strettamente correlato all’ordine necessario della loro generazione. Ed anche in questo caso numero e forma di ordinamento sono connessi da un preciso algoritmo che consente l’associazione in entrambe le direzioni. In realtà il sistema non copriva affatto esaustivamente i raga effettivamente impiegati, ed anche per i raga in uso il punto importante è che potevano essere considerati, dal punto di vista teorico, come forme dedotte. Una simile sistemazione veniva proposta proposta per avere una sorta di metro della realtà empirica.
Rispetto al Khandameru vi è dunque una significativa differenza. I settantadue tipi di raga di Venkatamakhin sono settantadue tipi melodici, e le loro differenze sono significative come tali. La schematizzazione teorica deve prendere le mosse da un modo di concepire l’ottava e da un pensiero di organizzazione delle varietà delle strutture intervallari conseguenti. L’ottava viene in effetti considerata come suddivisa in due tetracordi disgiunti, distinguendo poi tra raga con quarta «naturale» o quarta «diesizzata» . Poi si ragiona in modo puramente combinatorio individuando 6+6 possibilità di suddivisione per il tetracordo inferiore e 6 possibilità per il tetracordo superiore. A variare di posizione saranno naturalmente soltanto le due note intermedie dei tetracordi. Con ciò il numero complessivo dei raga è del tutto determinato (12 * 6 = 72) e non sarà difficile escogitare una procedura di associazione tra un numero ed una forma d’ordine.
Anche in questo caso ci troviamo di fronte ad una costruzione astratta, ma ciononostante non si può assolutamente prescindere da concetti musicali, quali sono le possibili differenze intervallari. Come abbiamo già notato invece, in rapporto al Khandameru, si può parlare di un unico tipo melodico, e poiché la questione è solo di permutazioni interne al tipo, si può arrivare ad astrarre dalla concettualità musicale per proporre la matrice come un metodo per il calcolo delle permutazioni per oggetti qualsivoglia.
Parte seconda
1. La serie dodecafonica concepita a partire dal triangolo di Sarngadeva
Ma è tempo di passare oltre. Il titolo di questo saggio suggerisce di fare una sorta di salto mortale dal triangolo di Sarngadeva alle serie dodecafoniche. In realtà non appena viene operata una descrizione della matrice e delle procedure corrispondenti, la possibilità di una generalizzazione appare piuttosto evidente. Ed allora si è tentati dal chiedersi: non potremmo forse proporre la serie dodecafonica all’interno di una matrice allargata da sette a dodici posti?
La sapienza storicistica respingerà forse questa tentazione quasi come una perversione, mentre io penso che a tentazioni di questo tipo ci si possa talvolta concedere per rimescolare le carte della teoria e come stimolo per una riflessione rinnovata. Il sistema di composizione con le dodici note è durato assai meno di quanto il suo autore avesse qualche volta osato sperare; mentre la teoria di quel sistema ci ha lasciato in eredità numerosi busillis sui quali è forse interessante continuare ancora un poco ad interrogarsi.
Abbiamo detto che è indifferente utilizzare la matrice di Sarngadeva per la scala sagrama o per il nostro do maggiore. Non si dovrebbe in essa cambiare nemmeno una virgola. Per la serie dodecafonica occorre invece modificare qualcosa - ma soprattutto riflettere sui problemi che si affacciano non appena ci poniamo su questa strada.
Vi è certo poco da dire sulle modificazioni da effettuare. Poiché abbiamo a che fare con dodici note, dovremo certo estendere corrispondentemente la nostra matrice e situare i valori nelle nuove caselle seguendo la regola generale della sua costruzione.
Un primo problema tuttavia sorge subito per il fatto che la serie dodecafonica non è vincolata allo spazio dell’ottava - e il superamento dell’ottava non può in ogni caso essere previsto nel nostro sistema di conteggio. È dunque inevitabile che una qualunque serie dodecafonica venga considerata come «ridotta» entro l’ottava. La forma normale sarà di conseguenza rappresentata dalla «scala cromatica» ed ogni spostamento verrà misurato rispetto ad essa. Se accettiamo tutto ciò senza disscussione, allora potremo con i nostri gettoni ed anelli, adeguatamente aumentati di numero, calcolare per ogni serie dodecafonica il numero ad esso associato. Inversamente, dato un numero inferiore al fattoriale di 12 potremo da esso cavare un ordine «dodecafonico» .
Prendiamo ad esempio la serie che sta alla base del Quintetto per strumento a fiati op. 26 di Schönberg[15]:
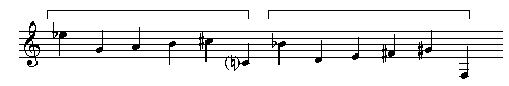
Operiamo anzitutto la riduzione entro l’ottava. A dire il vero, questa nozione non è affatto ovvia per il fatto che l’ottava entro cui operare la riduzione non è scritta per così dire nella serie stessa. Occorre perciò porsi su un terreno astratto, cosa che si può fare o utilizzando i nomi delle note nei quali non è contraddistinta nessuna altezza particolare oppure utilizzando numeri che contano le note e che indicano astrattamente la struttura intervallare. In tal caso si assumerà come innocua convenzione do = 1 (oppure do = 0). La forma normale potrà essere dunque rappresentata dalla lista di numeri
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
Di conseguenza la serie dell’op. 26 sarà rappresentata dalla lista seguente:
{4, 8, 10, 12, 2, 1, 11, 3, 5, 7, 9, 6}
A partire di qui, la matrice triangolare estesa a dodici posti (o una sua variante calcolistica), ci porta piuttosto speditamente, seguendo la via uddista, ad assegnare a quella serie dodecafonica il numero 252.026.617 come «numero di Sarngadeva» . Esso andrà poi inteso come indicante la posizione che quella serie occupa all’interno della serie delle 479.001.600 serie dodecafoniche possibili. Seguendo la via Nasta, si potrà poi ottenere dal numero 252.026.617 quella successione ordinata di numeri che rappresenta la serie stessa[16].
A dire la verità, l’operazione che abbiamo or ora compiuta non è così innocua come sembra ad un primo sguardo. Si presentano subito diversi dubbi che a loro volta generano una discussione, non solo sul senso di ciò che abbiamo fatto, ma necessariamente sul senso di ciò che propriamente è una serie dodecafonica, come fatto musicale specifico e come «oggetto matematico» . Ed è appena il caso di dire che è questa discussione che ci interessa, non certamente la pura e semplice assegnazione di un numero ad una serie dodecafonica qualsiasi.
Uno di questi argomenti lo abbiamo già sfiorato in precedenza nella questione della riduzione della serie entro l’ottava. Quando si parla di serie originale o di serie fondamentale nella terminologia dodecafonica si intende un «pensiero musicale» che sta a fondamento della composizione e che è esattamente quello che è. A partire da essa si determina in particolare quale forma della serie dobbiamo chiamare inversa, retrograda, o retrograda dell’inversa. Perciò difficilmente potremmo ancora parlare di serie originale se introduciamo una modificazione così notevole come quella della riduzione entro l’ottava, che naturalmente finisce con il modificare anche le direzioni degli intervalli. Nell’esempio precedente, il primo intervallo che era ascendente, diventa discendente nella riduzione entro l’ottava. D’altra parte, per quanto poco ciò venga notato, questa insistenza su una serie «originale» non ha senso dal punto di vista matematico formale. Ciascuno delle forme a specchio può essere assunta come base delle trasformazioni - trattandosi di una pura questione convenzionale che sta al di fuori del complesso strutturale da esse rappresentato.
Le cose stanno all’incirca come è illustrato nei seguenti disegni:
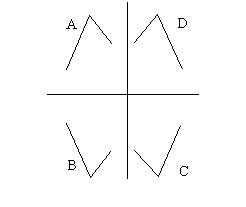
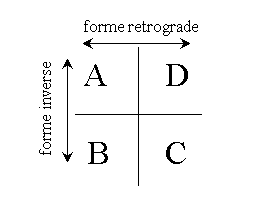
Se si considera A come come forma originale della serie, allora B sarà l’inverso e D sarà il retrogrado di A; C il retrogrado dell’inverso. Ma le determinazioni fondamentali sono il retrogrado e l’inverso. Formalmente il problema di una serie originale non sussiste. Una qualunque delle quattro forme tra loro collegate da queste relazioni può assolvere la parte di serie originale.
Nello stesso tempo, l’operazione di riduzione entro l’ottava non può essere considerata del tutto illegittima, tenendo conto del modo in cui la serie stessa può essere impiegata all’interno della composizione. Infatti una delle regole del «metodo» include esplicitamente la possibilità del salto di ottava di qualunque nota della serie fondamentale e delle serie derivate. Accade così che, se parliamo di una serie come fondamento di un brano musicale, siamo tenuti ad assumerla ed a proporla come immodificata; ma nella elaborazione compositiva della serie siamo invece liberi di proporre ciascuna nota indipendentemente dall’ottava nella quale si trova nella serie originale. Non è affatto escluso dunque che nella composizione si possa trovare la serie ricondotta entro lo spazio di un’ottava. In tutto ciò forse non si procede affatto «a rigor di logica» . In effetti si dovrebbe presentare la forma ridotta entro l’ottava come origine di varianti che contengono dei salti di ottava; ed a sua volta quella forma ridotta dovrebbe essere considerata a sua volta, non già come risultante di una «riduzione» , ma come prodotta a partire dall’effettiva forma normale, che altro non è appunto che la scala «cromatica» .
Se si è guidati dall’esprit de système si ragionerà indubbiamente così. Di conseguenza tutte le serie dodecafoniche si presenterebbero anzitutto come permutazioni della scala cromatica. Una delle prime considerazioni che viene fatto di fare seguendo il nostro singolare filo conduttore è che questo esprit - che è presente ovunque nel metodo compositivo dello Schönberg dodecafonico - in realtà ha su alcune questioni importanti una sorta di defaillance.
Ma si tratta propriamente di una defaillance o di qualcosa di diverso, che non può essere chiamato così? È un fatto che considerare la serie come una mera permutazione della scala cromatica sembra piuttosto urtante, per non dire dell’idea di una serie delle serie dodecafoniche, nella quale ciascuna serie dodecafonica ha una sua posizione determinata in anticipo.
L’idea di una derivazione algoritmica della serie si trova infatti nel contrasto più netto con la concezione della serie fondamentale come un pensiero musicale da cui il compositore si sente attratto e che rappresenta il germe della creazione musicale e dunque il luogo più segreto e più profondo da cui si dispiega la creatività. Questo modo di concepire la serie originale, insieme alla nozione di «senso della forma» a cui Schönberg tanto spesso si richiama come ad un vero e proprio «istinto» che non è in alcun modo riducibile a teoria, sono certamente nozioni di particolare importanza per comprendere la concezione della musica di Schönberg. E mentre per il musicista indiano le sistemazioni algoritmiche non introducono alcun turbamento all’interno della prospettiva entro cui egli si muove, e sono compatibili con un’idea «aperta» del comporre, l’inclinazione matematizzante che è indubbiamente caratteristica dello Schönberg dodecafonico così come la sua esasperata tendenza all’unità si arresta di fronte all’idea di una precostituzione matematica che toglierebbe alla serie fondamentale il carattere di espressione diretta del vissuto del compositore - la fonte segreta e misteriosa da cui scaturisce l’opera, ciò da cui essa è «ispirata» .
Per quanto riguarda invece il rapporto tra le serie e la scala cromatica, occorre intanto osservare che non tutte le serie generate come sue permutazioni verrebbero accettate sotto il profilo musicale. Vi sono delle limitazioni significative, a cominciare dalla regola esplicita che vieta più semitoni successivi oppure la regola implicita che vieta o «sconsiglia» le serie che contengono in successione suoni che formano triadi consonantiche.
Limitazioni di questo tipo sono naturalmente della massima importanza per comprendere il senso della proposta teorica e musicale dodecafonica. Ma non sono tali da mettere realmente in crisi le considerazioni precedenti, per il fatto che si potrebbe semplicemente ammettere che la serie totale delle serie dodecafoniche è sovrabbondante rispetto alle serie «ammissibili» .
Più interessante è invece mettere in risalto un altro aspetto che proprio il riferimento al triangolo di Sarngadeva aiuta a mettere a fuoco. Abbiamo detto che, in fin dei conti, nel Khandameru le permutazioni riguardavano un unico tipo melodico - una scala con un determinato schema intervallare - e che di conseguenza nella proposta di «enumerarle» era contenuto il pensiero del dominio di tutte le possibili configurazioni delle note all’interno di quel tipo. In certo senso potremmo dire che in ogni caso ogni configurazione è soltanto una permutazione.
Lo stesso problema si pone in modo del tutto diverso in rapporto alla serie dodecafonica. Benché si possano considerare - con le limitazioni del caso - le serie dodecafoniche come permutazioni della «scala cromatica» , tuttavia quest’ultima non merita affatto di essere caratterizzata come «tipo melodico» . In realtà l’insegnamento scolastico spesso non attira a sufficienza l’attenzione sulla netta differenza tra scala diatonica e scala cromatica, come se si trattasse di due «scale» allo stesso titolo e nello stesso modo - come se differissero soltanto per la grandezza e la distribuzione degli intervalli. Quest’errore è d’altronde, dal punto di vista teorico, rafforzato dalla tematica dodecafonica, che comporta la negazione del fenomeno autentico del cromatismo, nello stesso momento in cui richiede la massima indipedenza delle dodici note l’una dall’altra, mentre il cromatismo richiede al contrario una forma particolare e particolarmente forte di «interdipendenza» connessa alla possibilità della transizione. La scala cromatica, che dovrebbe rappresentare, nel quadro delle nostre considerazioni, la «forma normale» , non è un tipo melodico proprio perché essa è riconducibile alla pura transizione, che può cominciare in un luogo qualunque e terminare in un altro luogo qualunque, senza modificare il proprio profilo, senza delineare alcun melos. Essa è, in certo senso, priva di carattere. Ed è invece proprio alle sue permutazioni, eventualmente variate attraverso dislocazioni di ottava, che sembra spettare il carattere di una molteplicità di tipi melodici. Siamo dunque tenuti a dire esattamente l’inverso di ciò che abbiamo or ora osservato in rapporto al Khandameru.
Ma il groviglio di problemi non finisce qui. Abbiamo parlato or ora della serie dodecafonica come di un tipo melodico. Su di ciò credo che siano in molti ad obiettare. Intanto si continua a ripetere che con la dodecafonia viene meno la distinzione tra melodia e armonia. Di conseguenza non vi sarebbe motivo di considerare una serie orizzontalmente piuttosto che verticalmente. Il parlare della serie come tipo melodico sarebbe senz’altro erroneo. Si rischierebbe di fare di una serie qualcosa di simile ad un «modo» .
Su queste affermazioni credo che sia lecito almeno parzialmente dissentire. Ciò che viene meno è naturalmente la distinzione tra melodia e armonia così come si presenta nell’ambito del linguaggio tonale. Più in generale l’ordine orizzontale della serie può, dal punto di vista della prassi compositiva, essere proposto anche «verticalizzato» . Ma di qui non si può affatto trarre come conseguenza che la serie possa essere considerata indifferentemente rispetto alla simultaneità ed alla successione. Si confonde qui l’impiego previsto dal metodo, che autorizza l’impiego simultaneo, con ciò che la serie è come fatto uditivo specifico; e questa confusione viene rafforzata dall’oscillazione tra un’idea astratta della serie come mera forma relazionale - e quindi come entità matematica - ed un’idea della serie come qualcosa che risuona concretamente e che risuonando ha un certo carattere piuttosto che un altro. Considerando la serie come un oggetto formal-matematico, quindi come un complesso di oggetti in genere che stanno fra loro in determinate relazioni, viene meno addirittura la sensatezza della distinzione tra una dimensione verticale ed una orizzontale per il semplice fatto che in una simile considerazione non vi è in via di principio né contemporaneità né successione. Altrimenti stanno le cose dal punto di vista percettivo. La prova più persuasiva della differenza tra ordine verticale e ordine orizzontale, che continua ostinatamente a resistere ad ogni negazione teorica, sta nel semplice fatto che una serie qualsiasi somiglia anche troppo a qualsiasi altra se le sue note vengono fatte risuonare tutte insieme: come è più che ovvio! Eppure vi è chi, parlando della serie, afferma che essa viene proposta «melodicamente» per pure ragioni di «comodità» .
«Per comodità operativa il musicista fissa la «serie dodecafonica» nella successione orizzontale, al fine di stabilire i rapporti di altezza, cioè gli intervalli, tra suono e suono; ma la «serie» così fissata non rappresenta però un principio tematico, una sorta di Leitmotiv, sul quale la composizione è destinata a svilupparsi» [17].
Ma di quale «comodità» si tratta? La serie, proprio come pensiero musicale, che contiene certamente in quanto tale un rimando alla situazione percepita, è essenzialmente orizzontale, quindi è in senso ampio, melodia. E non mancano certo dichiarazioni assai significative da questo punto di vista: è lo stesso Schönberg, che proprio mentre illustra la possibilità di impiegare «il raggruppamento di alcune note in armonie» sottolinea che «la serie fondamentale funziona come se fosse un motivo» [18]; e lo scritto in cui si trova questa frase, e che rappresenta forse il suo scritto più impegnativo sulla teoria della tecnica dodecafonica, si chiude con questo icastico richiamo al Leitmotiv wagneriano: «Penso che quando Richard Wagner introdusse il suo Leitmotiv - con lo stesso scopo per cui io ho introdotto la mia Serie Fondamentale - deve aver detto: «Che l’unità sia fatta» » . [19]Un altro elemento di conferma si può trovare nel fatto che Schönberg, negli esempi di serie che egli discute, propone cesure e segni di articolazione. Ad esempio, nella serie precedentemente citata dell’op. 26, viene fatta cadere una cesura nel mezzo. Anche se queste cesure sono giustificabili a partire dalla struttura formale, non sarebbe giusto affermare che esse siano derivabili da essa; così come che esse siano derivabili dalla conformazione percettiva come tale. È appunto un «pensiero musicale» che sceglie, all’interno di diverse possibilità, le articolazioni interne che debbono essere evidenziate. E naturalmente queste cesure sarebbero dei puri nonsensi se fossero proposte sulla serie proposta in forma di accordo.
È dunque abbastanza giusto considerare la serie anzitutto così come decorre nell’ordine temporale del prima e del poi - e quindi qualcosa di simile ad una melodia, ad un tema o ad un motivo. Ma questo aspetto si modifica profondamente sia se consideriamo il suo trattamento compositivo, sia se pensiamo alla forma astratta in cui la serie può essere «pensata» e che fa venire meno il problema stesso dell’ordine temporale. Vi sono diverse importanti ragioni, sulle quali non è il caso qui di soffermarsi, che non rendono assolutamente possibile l’assimilazione della serie ad un modo.
Tuttavia è proprio facendo riferimento a questo aspetto della questione, che si spiega come mai Schönberg possa essere talora elogiato dalla musicologia indiana o come questa possa addirittura rivendicare improbabili anticipazioni nella propria tradizione musicale. In un testo che si propone esplicitamente di contribuire alla conoscenza reciproca della cultura musicale indiana e di quella europea, intitolato The structure of music in raga and western systems, Raja Ramanna osserva che, nella musica indiana, la dodecafonia schönberghiana sarebbe stata anticipata di alcuni secoli[20]. L’autore pensa qui al sistema di Venkatamakhin ed ai raga, concepiti come tipi melodici, come motivi di base di una costruzione musicale; e risulta a lui naturale considerare la serie dodecafonica secondo questa stessa angolatura. Il merito di Schönberg sarebbe stato dunque quello di superare la miseria dei due modi della musica tonale riportando nella musica europea un’autentica molteplicità. Ma questa molteplicità non è forse presente da secoli, attraverso i raga, nella musica indiana?
I teorici europei alla fine dell’ottocento, osserva Ramanna «cominciarono a sottolineare che la stessa tonalità non era essenziale per la musica e non era basata su alcuna considerazione razionale e le scale maggiori e minori non erano sufficienti per esprimeri i pensieri al di là di quelli dei compositori del XIX secolo. Fu a questo stadio l’armonia atonale venne proposta da Schönberg, che fa rivivere Venkatamakhin dopo quasi quattrocento anni. La modernità di Venkatamakhin dal punto di vista europeo è davvero sbalorditiva» [21].
Lo stesso autore fa notare che, quando verso la fine del secolo XIX si pose il problema di una «armonizzazione» dei raga, del resto sotto l’influsso della musica europea - non si andò in direzione delle triadi tonali, quanto piuttosto di una proiezione nella simultaneità dell’ordine successivo delle note del raga, secondo una procedura che sembra essere l’esatto rovesciamento nel rapporto armonia-melodia caratteristico di un ambito linguistico tonale. Una simile proiezione può essere possibile solo se viene liberamente ammessa anche la presenza di dissonanze.
Vi sono qui numerosi equivoci, che sono tutti per lo più da ricondurre ai due aspetti che abbiamo appena richiamati, alla pratica compositiva dodecafonica che non va certamente in direzione di una valorizzazione dell’elemento melodico; ed all’idea di uno spazio sonoro, in rapporto alla serie, che probabilmente deve essere caratterizzato più che relativamente alla serie fondamentale considerata nella sua individualità concreta, ad una struttura relazionale astratta, che possa comprendere anche le forme modificate e le trasposizioni. Naturalmente la questione di un diverso rapporto con la consonanza e la dissonanza resta sul tappeto - ma alla comprensione di questa diversità giovano assai poco confronti di questa natura. Ed ancor meno giovano le considerazioni sull’ «armonizzazione» .
Nel metodo dodecafonico la dimensione «armonica» viene in realtà soppressa per il fatto che non solo si sopprime l’impiego armonico della triade, ma anche perché gli accordi in genere assumono il carattere di eventi sonori in via di principio sullo stesso piano dei suoni singoli e non hanno in ogni caso carattere di armonizzazioni o di accompagnamenti. Il fatto che essi siano costituiti da segmenti della serie non modifica certo questo stato di cose. Ciò che sorprende nelle considerazioni di Ramanna è che si vada a citare con tanti equivoci Schönberg e la dodecafonia, e non si faccia invece il minimo cenno al modalismo che ha così grande importanza nella musica novecentesca e che in alcuni casi - penso naturalmente a Messiaen - ha anche un rapporto musicalmente concreto con la musica indiana.
Se tanti sono i problemi emersi, non è stato forse inutile il gioco di estendere il Khandameru alle serie di dodici note.
[1] Sarngadeva, Sangitaratnakara, testo sanscrito e traduzione inglese di R. K. Shringy, vol. I, Varanasi 1978, p. 208. Talora il titolo viene reso con Oceano di gemme della musica. «Ratnakara» può essere tradotto con «mare, oceano» ; oppure con «miniera di gemme» (jewel-mine, sea, ocean M. Monier-Williams, A Sanskrit-English Dictionary, Oxford 1899 (1990)) - Sono debitore di molti stimoli per l’argomento di questo saggio, oltre che di un concreto aiuto bibliografico, a Francesca Dell’Acqua, che ha svolto nel 1994-95 una tesi di laurea intitolata «Teorie della musica e filosofia nel Sangitaratnakara di Sarngadeva» presso l’insegnamento di Filosofia Teoretica da me tenuto, con correlazione di Carlo Della Casa. - Una stesura preparatoria di questo lavoro è stata presentata al convegno organizzato dal Seminario Permanente di Filosofia della musica, Dipartimento di Filosofia dell’Università degli Studi di Milano, svoltosi a Gargnano, Palazzo Feltrinelli, 29 settembre-1 ottobre 1997.
[2]. Siamo nel XIII secolo, in un’epoca che viene considerata di transizione tra la musica antica e la musica medioevale. M. R. Gautam propone di distinguere la storia della musica indiana in tre grandi fasi, la musica antica, medioevale e moderna. Le prime due possono essere considerate come concluse approssimativamente nel XIII secolo e nel XVIII secolo, mentre la terza arriva ai nostri giorni. M. R. Gautam, Evolution of Raga and Tala in Indian Music, New Delhi 1993, p. IX. Sarngadeva viene trattato nel cap. IV, pp. 61 sgg.
[3] Sangitaratnakara, 63c-71, cit. p. 208-220.
[4] «Uddista is literally the note-series indicated, and what is sought to be found out from the permutation indicator is its serial number» , ivi, p. 214.
[5] «Nasta of the text literally means «that which is destroyed» , but the term is figuratevely employed in a technical sense. Nasta refers to that note-series (tana) the tonal form of which is lost sight of, but in respect of which the serial number and the type... is given in the order that its tonal form may be discovered with the help of the note-series indicator» - ivi, p. 218.
[6] Riferiamo qui di seguito le spiegazioni di Sarngadeva nella traduzione inglese:
IV. Khandameru (permutation-indicator)
1. The construction of the permutation-indicator (63c-66b): Let there be seven series of squares commencing with seven squares and ending with one, arranged one below the other. Let no. 1 be written in the first square of the first serie among them and let there be zero in the other squares. Pebbles, corresponding to the number of tones in the note-series in question, may be placed in those very squares. (63c-64). Let the sum total of the numbers of the last squares of the antecedent serie be written below the zero in the subsequent series progressively in the respective squares, e. g. one (in the first instance); while in the squares below that in vertical order, let the sum be multiplied by the number of the square concerned and the resultant written below that. This is considered to be the «permutation-indicator» (khandameru). (65-66b)
2. The procedure for finding out the indicate note-serie (uddista): 66c-68b: Let the pebble be placed in the column-square below according to the number of the last note of the indicated note-series obtaining backwards with refernce to the last note of its original order. The pebble movement starts with the last note and is ordered by dropping the note ascertained progressively. The number of the indicated note-series would be obtained by adding up the figures (of the squares) covered by pebbles»
3. The procedure for finding out the missing note-series (nasta): (63c-70): Let the initial pebbles be placed in the respective squares, the sum of the figures of which would constitute the number of the ’missing note-series’ includsive of the figure1 in the first column square. The note-positions of the missing note-series are to be determined from the pebble-squares, the serial number of the squares down below being indicative of the relative backward position of the respective notes with reference to the last note of the original order; while the rule for dropping the ascertained note ecc. would apply as before. (68c-70).
[7] Sarngadeva attua metodi analoghi al Khandameru anche per l’organizzazione sistematica delle possibilità ritmiche (tala). Sull’argomento: Subhadra Chaudhary, Time Measure and compositional types in indian music, A historical and analytical Study of Tala, Chanda and Nibaddha Musical forms, trad. ingl. di Hema Ramanathan, Aditya Prakashan, New Delhi 1997, pp. 85 seg.
[8] Neil Sorrell e Ram Narayan, Indian music in performance, con pref. di Y. Menuhin, University Press, New York 1980.
[9] ivi, p. 70.
[10] ivi, p. 73.
[11] ivi.
[12] ivi, p. 74: «The relationship between exercise and 'real' music is very interesting and of central concern to this chapter. As I have implied so far, there is not the separation between these categories in Indian music that we find in western Music» .
[13] ivi, p. 70.
[14] ivi, p. 74. Cfr. anche p. 91: «The increasing length and musical interest of these examples shows how simple exercises can be spontaneously transformed into something more sophisticated. The imagination of the musician and his skill in improvisation enable him to extend a small amount of material into longs sections of music. Practice becoms virtually indistinguishable from real performance and his creative process is at the heart of North Indian classical music» .
[15] Questa serie viene discussa da Schönberg nella sez. VII Composizione con dodici note, in Stile e idea, trad. it. di M. G. Moretti e L. Pestalozza, Milano1975, pp. 116 sgg.
[16] Per ciò che riguarda in modo del tutto generale i metodi combinatori in rapporto a successioni ordinate di suoni, cfr. Luigi Verdi, Organizzazione delle altezze nello spazio temperato, Treviso 1998.
[17] L. Rognoni, La scuola musicale di Vienna, Einaudi, Torino 1966 p. 90.
[18] A. Schönberg, Composizione con dodici note, in Stile e idea, trad. it. di M. G. Moretti e L. Pestalozza, Milano1975, pp. 111.
[19] ivi, p. 140.
[20] Raja Ramanna, The structure of music in raga and western systems, Bombay 1993. p. 160.
[21] ivi p. 160. Cfr. anche p. 167.

