Una breve sintesi di questo testo è stata proposta nel corso della Giornata di Studio sul tema "Musica e natura" promossa in data 15 marzo 2001 dal "Seminario Permanente di Filosofia della musica" in collaborazione con il Dipartimento di Filosofia dell'Università degli Studi di Milano, Scuole Civiche di Milano e Centre Culturel Français de Milan. Questo saggio è stato pubblicato in "Sonus. Materiali per la musica moderna e contemporanea" (dir. da Antonio De Lisa), n. 21-22 dic. 2002 - Data di immissione in questo archivio: 2002
Commento di Maria Cecilia Farina

Giovanni Piana
La composizione armonica del suono e la serie delle affinità tonali in Hindemith
1. Introduzione
4. La procedura di spostamento di grado
5. Le tre fasi della deduzione della Serie 1
6. Soppressione del fisicalismo
7. La nozione di affinità tonale
Considerando le vicende musicali del secolo XX, si potrebbe essere indotti a pensare che esse hanno come contraccolpo, dal punto di vista della teoria musicale, il definitivo tramonto dei tentativi di fondazione oggettiva-assolutistica dell’espressione musicale: ciò vale già naturalmente per la produzione musicale della prima metà del secolo, ed a maggior ragione per la seconda metà. La grande varietà di percorsi che la musica del secolo XX ha tracciato e perseguito tende ad assumere il carattere di un gigantesco dato di fatto che sommerge l’idea stessa di una possibile giustificazione oggettiva delle regole del comporre o degli ordinamenti predisposti dei suoni, degli intervalli e delle loro relazioni. Si potrebbe arrivare ad affermare che viene meno persino l’oggetto stesso da fondare e da giustificare, e questo per il semplice fatto che la nozione di «regola del comporre» è diventata sempre più evanescente e la prevalenza dell’interesse verso il timbro tende a mettere in secondo piano ogni problematica relativa al suono-nota, al suono come altezza ed ai suoi ordini possibili.
Ha forse senso oggi discutere sugli intervalli buoni e cattivi, giusti o sbagliati, perfetti o imperfetti? Oppure sulle consonanze o le dissonanze e sui loro gradi, sulle strutture scalari e sui modi di generarle, sulle regole possibili di una «buona» melodia o di una buona concatenazione armonica? A maggiore ragione dunque sembra venire meno l’interesse delle fondazioni oggettive, delle fondazioni assolute.
Questo venir meno è tutt’altro che cosa di poco conto nella storia della musica e della sua teoria! Questa storia è stata fin dall’inizio segnata proprio dall’idea che la musica non sia affatto soltanto un’estrosa pratica di manipolazione dei suoni, regolata al più dal piacere che si può trarre da essa, ma che in questa pratica si facciano valere dei nessi profondamente giustificati. Questo problema si orienta anzitutto in direzione dei rapporti tra musica e matematica, tra relazioni musicali e relazioni numeriche, come se le prime fossero in grado di manifestare sul piano della percezione rapporti astratti, afferrabili solo intellettualmente. Un simile orientamento si può dire nasca con la nascita stessa della riflessione sulla musica, quindi dal tempo dei tempi, in Europa, ma anche in Oriente, in Cina e in India. Nella tradizione europea esso si mantiene immutato nei suoi termini fino almeno alla fine del secolo XVII : poi subentra la scoperta che determina la svolta che ci consente di parlare non più soltanto di una fondazione oggettiva, ma propriamente di una fondazione «naturalistica». Si tratta della scoperta degli armonici e della legge interna che li regola: è questa scoperta che segna il passaggio da una problematica fondazionale tutta volta al versante matematico ad una problematica fondazionale volta invece su un versante fisico.
Il suono che appare all’orecchio come suono semplice è costituito in realtà da un viluppo di suoni, l’altezza con cui noi lo udiamo e lo identifichiamo è correlata ad una frequenza, che tuttavia va considerata solo come una frequenza dominante all’interno di un fascio di frequenze di intensità decrescente. Un suono, considerato dal punto di vista fisico, è un evento complesso, e si fa subito strada l’idea che analizzando questo evento ed in particolare districando le sue componenti si possano strappare al suono i suoi segreti, si possano svelare le ragioni delle affinità e delle differenze tra essi e rendere conto dei loro ordinamenti privilegiati, e quindi anche dei loro possibili «valori» musicali.
Vi è una assai significativa differenza tra giustificazione aritmetica e giustificazione fisica, che viene spesso trascurata nelle esposizioni correnti e sulla quale invece è opportuno richiamare vivacemente l’attenzione.
Il numero può essere proprietà comune di cose molto differenti. Si può attribuire un numero a cose concrete, a dei «corpi», ma anche a entità incorporee, a nozioni che non hanno nulla a che vedere con la corporeità. Nella grecità la relazione al numero era stata posta con chiarezza dal pitagorismo in rapporto agli intervalli fondamentali della consonanza di quinta, di quarta e di ottava, anzitutto indubbiamente attraverso l’osservazione empirica e quindi con riferimento a corpi risuonanti. Non era stato tuttavia possibile ancorare il rapporto numerico al corpo sonoro, al contrario tutto sembrava suggerire e rafforzare l’idea che il corpo sonoro fosse indifferente e l’intera responsabilità del risultato sensibile fosse dovuto al rapporto numerico come tale, ad una sua peculiare virtù. Un flauto è una cosa assai diversa da un corda tesa, eppure la validità del rapporto non teneva conto di questa diversità. Cosicché da un lato veniva ritenuta significativa la relazione numerica in se stessa, dall’altro questa significatività doveva essere riferita non ad una proprietà strettamente dipendente dal modo concreto di produzione del suono, ma al contrario il rapporto numerico si arricchiva di senso per il fatto che esso puntava al di là del suono verso cose rispetto ad esso eterogenee, ed anzi verso il mondo nella sua totalità. La comunanza nel numero è una comunanza che non riguarda la materia di cui sono fatte le cose, ma rimanda piuttosto alla loro comune appartenenza alla totalità stessa del mondo. Inversamente, al di là della varia superficie delle cose, della disparatezza e della possibile dispersione, il numero sembra prestarsi alla funzione di fornire l’impalcatura necessaria per tenerle insieme e vincolarle in una stabile unità. Si comprende dunque che il movimento in questa direzione tenda ad assumere valenze metafisiche: la relazione tra musica e numero rappresenta allora la via maestra per asserire una legalità interna del musicale che avrebbe le sue radici nella legalità del mondo stesso.
La scoperta degli armonici si annuncia già sulla base dell’osservazione delle corde vibranti, soprattutto in connessione con i fenomeni di risonanza, per poi consolidarsi sempre più ed assumere un profilo teoricamente ben determinato con la consapevolezza, definitivamente acquisita, intorno all’origine del suono dalle vibrazioni di un corpo ed in particolare con la raggiunta capacità tecnica di «contarle», istituendo così una precisa relazione tra altezza percepita del suono e frequenza delle vibrazioni del corpo che lo emette. Tutto ciò conduce ad uno spostamento teorico estremamente significativo: l’idea di una fondazione oggettiva del musicale tende a liberarsi da un impianto metafisico, per riproporsi come una idea che deve svilupparsi avendo di mira l’interno del suono stesso, la sua costituzione fisica, la sua natura come oggetto fisico. In questo senso dunque, con stretto riferimento alla fisica del suono, si può parlare in questo contesto di naturalismo e, in particolare, di fisicalismo. Il suono viene riportato alle sue cause naturali, alle vibrazioni dei corpi sonori; ed i numeri assumono asssumono allora un significato non in quanto rappresentativi di forme relazionali astratte, ma come numeri che contano la frequenza di queste vibrazioni. Finché il rapporto numerico viene istituito sulla base di osservabili (come nel caso dell’osservazione e della misurazione della lunghezza delle corde), senza che tuttavia sia possibile collegare solidamente il fenomeno percettivo a precisi eventi che si verificano nel corpo che lo genera, quel rapporto fluttua in certo senso a mezz’aria arrivando a sostituirsi a quegli eventi come se il numero stesso avesse peculiarità «sonore». La dizione di «numeri sonori» (Zarlino) rende conto con grande efficacia di questo orientamento del pensiero. Ma esso non può che indebolirsi ed attenuarsi quando la relazione numerica diventa una pura e semplice relazione tra frequenze, e quindi tra eventi fisici chiaramente circoscritti. Senza scomparire del tutto. Di fatto attraverso la misurazione delle frequenze vengono confermate ed in certo senso portate alla massima evidenza le antiche proporzioni pitagoriche per le consonanze fondamentali; e nella considerazione degli armonici vengono persino convalidate innovazioni ottenute esclusivamente sul filo di considerazioni formal-aritmetiche, completamente immerse nello spirito del pitagorismo antico, come nel caso della «terza zarliniana». Un pitagorismo nascosto può sempre riaffiorare in una concezione fisicalistica, che in via di principio dovrebbe aver lasciato interamente alle proprie spalle la metafisica del numero e le speculazioni numerologiche.
Ma ancora più rilevante, dal punto di vista musicale e in rapporto alla storia del problema, è il fatto che la scoperta degli armonici avviene - all’inizio del secolo XVIII - simultaneamente all’affermarsi del linguaggio della tonalità e che questa affermazione può sostenersi, dal punto di vista della fondazione teorica proprio su di essa: i primi armonici squadernano sul tavolo del teorico proprio la «triade maggiore» che rappresenta la vera e propria articolazione fondamentale dello spazio sonoro considerato dal punto di vista del linguaggio tonale.

La divisione dell’ottava sui pilastri della triade sembra rappresentare la proiezione della struttura interna del suono singolo. Il punto di vista dell’ «armonia» triadica che si è già affermato ampiamente sul piano musicale sembra così trovare garanzia permanente di validità nella «natura fisica» del suono.
Non vi è certo da meravigliarsi se per un paio di secoli un possibile fondamento dei fenomeni musicali negli armonici abbia affascinato musicisti, teorici della musica e scienziati interessati alle problematiche fisiche e musicali. Ma proprio questa relazione con il linguaggio della tonalità è destinato alla fine ad indebolire la tenuta complessiva del problema fondazionale posto in questo modo.
Anzitutto esso rischia rimettervi la propria generalità. Secondo una simile prospettiva, infatti, non vi è da un lato l’ambito dei fenomeni fisici e delle loro legalità e dall’altro l’intero universo delle possibili manifestazioni musicali.
La fisica del suono si assume invece la responsabilità di farsi garante di un particolare linguaggio musicale; e ciò implica che quel linguaggio debba essere considerato come il linguaggio migliore, nel senso del linguaggio più adeguato alla vera essenza del suono come oggetto naturale. Ed allora va da sé che quando, seguendo le proprie logiche di sviluppo interne, che sono di ordine espressivo, quel linguaggio giunge al suo tramonto, la relazione fondazionale con la fisica del suono si possa presentare come un grave errore e come fonte di confusione. La «crisi» del linguaggio tonale sembra coinvolgere anche il problema di ogni fondazione naturalistica della musica, un problema dunque che - dovremmo sospettare - varcherebbe appena la soglia del secolo XX, quando quella crisi giunge ormai alle sue più vistose manifestazioni.
Le cose tuttavia non stanno esattamente così. Intanto non vi è dubbio che l’interesse per la fisica del suono è stato grandissimo nell’intero corso del secolo XX, stimolato anche dai grandi progressi scientifici che sono stati realizzati in questo campo e dal corteo di straordinarie applicazioni tecnologiche che da questi progressi sono derivate. Anche i musicisti si sono lasciati coinvolgere da questo interesse indubbiamente in misura straordinariamente più ampia che per il passato per ragioni spesso strettamente inerente alle nuove pratiche musicali ed all’uso consapevole dei nuovi mezzi tecnici di produzione e di ricezione del suono. L’idea del suono come un complesso da analizzare e dalla cui analisi possa in qualche modo derivare la musica stessa ha continuato ad esercitare il proprio fascino ed ha conosciuto, in tempi abbastanza recenti, persino una concretizzazione musicale, nel cosiddetto «spettralismo» che inserisce questo aspetto fisico - la composizione armonica dei suoni - in un progetto espressivo, considerandolo come una fonte possibile di organizzazione del brano musicale [1] .
Se poi guardiamo alla questione propriamente teorica, si può dire che sia definitivamente tramontata l’idea che vi possa essere un legame tra natura e linguaggio tonale tanto forte e tanto semplice come sembrava suggerito dalla presenza negli armonici della triade maggiore. Tuttavia l’intera questione di una fondazione naturalistica è stata ripresa in molteplici direzioni e con scopi e motivi diversi.
Tra queste riprese una posizione in certo senso estrema è quella di Paul Hindemith - ed è di essa che ci occuperemo in questo saggio.

Il titolo dell’opera teorica di Hindemith Unterweisung im Tonsatz, datata 1937 [2] si potrebbe forse tradurre in italiano con «Istruzioni per il comporre». In esso viene messo in rilievo soprattutto l’aspetto «didattico» che è proprio della seconda parte dell’opera e che questo trattato ha in comune con l’altro grande trattato novecentesco, l’Harmonielehre di Arnold Schönberg. Ma come nei trattati degli antichi maestri, anche in Hindemith la parte pratica è preceduta da una parte speculativa nella quale si presenta un tentativo di riportare le relazioni fondamentali della musica a fatti di ordine fisico-acustico. Si tratta di un tentativo realmente massiccio, che forse non ha eguali nella storia della teoria musicale, vorremmo quasi dire, per ostinazione e complessità della procedura proposta. Esso riprende la riflessione sulla composizione armonica del suono, effettuando il tentativo di derivare di qui (e quindi giustificare), i dodici suoni della «scala cromatica» unitamente alla derivazione e giustificazione dei gradi di affinità tonale. Questo progetto si realizza con la esibizione di quella che Hindemith chiama Serie 1. Non meno importante è la sperimentazione e la riflessione sui suoni differenziali o suoni di combinazione, che assumono rilevanza in funzione di un nuovo modo di considerare l’intervallo, da cui consegue un radicale rinnovamento della concezione dell’accordo e dell’idea di nota fondamentale. Anche questo aspetto della ricerca hindemithiana mette a capo ad una serie che egli chiama Serie 2.
L’intera ricerca avviene nel quadro dell’apprestamento dei principi elementari di una teoria analitica che aspira alla massima generalità e che assume le vesti modeste di un trattato di contrappunto; e nello stesso tempo essa può essere interpretata anche come volta a definire il metodo compositivo dell’autore. Come si vede, c’è molto su cui riflettere! I nostri interessi, sul cui sfondo vi è il problema della partizione dello spazio sonoro, si possono tuttavia limitare ad una illustrazione e ad una discussione sul percorso che conduce alla formazione della Serie 1.
Ciò che va in primo luogo messo in rilievo è la novità nel modo di considerare la composizione armonica del suono per scopi fondazionali. Una tesi naturalistica molto forte potrebbe pretendere di ritrovare negli armonici non soltanto i tre suoni della nostra scala diatonica che formano la triade maggiore e che sono del resto a portata di mano, ma anche gli altri quattro suoni di cui essa consta, in modo tale che la validità già confermata musicalmente ed eventualmente rafforzata da considerazioni di ordine matematico, sia confermata anche dal punto di vista della fisica del suono.
Non è difficile tuttavia rendersi conto che il compito potrebbe aver senso solo a patto che vi sia una qualche procedura ben definita che consenta il raccoglimento sistematico degli armonici «validi» (va da sè che in questo genere di considerazioni si cerca ciò che per altra via si è già trovato). In effetti la legge elementare degli armonici insegna che la frequenza dell’n_esimo armonico sarà pari alla frequenza del suono assunto come base moltiplicato per n. Ciò che interessa, in rapporto al nostro problema, non è naturalmente lo sviluppo degli armonici come tale, ma la partizione che risulta proiettando questo sviluppo entro l’ottava il cui estremo inferiore è il suono-base. Tale proiezione si ottiene attraverso la divisione per 2 iterata sino ad ottenere un valore compreso tra 1 e 2, corrispondendo ogni passo allo spostamento di un’ottava verso il basso.
Conveniamo di chiamare questa operazione «procedura di riduzione» (entro l’ottava).
Ovviamente, operando in questo modo, si troveranno tra gli armonici valori già trovati in precedenza, ma il punto importante è che procedendo sempre più oltre nello sviluppo degli armonici si otterranno valori sempre nuovi e ciò significa che si avrà una partizione dell’ottava sempre più fine, gli intervalli diventeranno sempre più piccoli fino a riportare l’ottava di base, considerata dal punto di vista percettivo, all’unità «continua» del flusso. Va da sé che prima o poi si incontreranno anche i valori cercati, ma proprio questa circostanza rende una simile procedura del tutto insignificante. Infatti vi sono valori che debbono essere scartati, e non vi è alcun preciso criterio per questa selezione che non sia quello del confronto con i valori ritenuti musicalmente validi. Il fatto che poi, proseguendo a piacere verso gli armonici superiori, si arrivi ad una divisione sempre più fine dell’ottava, significa nello stesso tempo che seguendo una simile via qualunque modello scalare potrebbe essere giustificato [3] . La giustificazione di tutto equivale alla giustificazione di nulla.
Affinché il ricorso agli armonici possa dare il risultato fondazionale che si ricerca attraverso di esso, è necessario dunque che il reperimento degli armonici musicalmente validi abbia il carattere di una «deduzione» e cioè avvenga secondo una regola rigorosamente determinata che sia in grado di operare essa stessa una selezione di valori «coincidenti» con quelli a cui si è già riconosciuto una validità musicale. Naturalmente questa coincidenza di per sé non prova ancora nulla. E tuttavia quanto più forte sarà la coincidenza tanto più forte potrà essere considerata l’ipotesi che essa non sia casuale, ma che vi sia invece una relazione effettiva tra le due serie di valori - e precisamente che la seconda sia «fondata» nella prima, e che quindi la scala musicale sia l’affiorare alla superficie sensibile della struttura fisica profonda del suono.
Come sarebbe bello allora se la regola fosse la stessa che sviluppa gli armonici dal suono ovvero se accadesse che le note della scala fossero dispiegate dai primi armonici ottenuti, l’uno dopo l’altro, eliminando eventuali raddoppi; e addirittura se l’ordine secondo cui essi vengono ottenuti fosse a sua volta indicativo di una «distanza» crescente rispetto alla nota-radice, come sembra accadere almeno nei primi passi, dove la quinta precede la terza nell’ordine di acquisizione! L’ambito delle giustificazioni si estenderebbe allora dagli intervalli puri e semplici alle loro relazioni. Ma come abbiamo detto non accade affatto così: fino al sesto armonico possiamo forse compiacerci di aver soddisfatto entrambe le condizioni, ed il risultato, è notevole perché squaderna la triade maggiore. Purtroppo basta fare un passo oltre per avere un dura smentita alle nostre speranze. Il settimo armonico - anzi «il funesto settimo armonico», per usare l’espressione di Hindemith [4] - si trova in un rapporto di 7/4 (pari a 969 cents) con la nota-radice, un rapporto che non è considerato valido «nel nostro sistema musicale (Tonsystem)» [5]. Hindemith nota che si tratta di un si bemolle fortemente «calante» [6], ma rende subito avvertiti della improprietà di simili espressioni riferite agli armonici. Proprio mentre ci si accinge a fare incontrare considerazioni musicali con considerazioni fisiche occorre prestare attenzione nel non confonderle l’una con l’altra. Gli armonici non ne sanno nulla delle nostre decisioni musicali, il settimo armonico è esattamente quello che è ed in rapporto ad esso, come in rapporto a tutti «i suoni naturali degli ipertoni», non possiamo affatto dire che essi siano «troppo alti» o «troppo bassi» [7]. È giusto invece affermare che vi sono suoni naturali che non trovano posto nel nostro sistema. Occorre inoltre considerare che quanto più si sale nella successione degli armonici, tanto più evanescente diventa la nozione di armonico dal punto di vista fisico, per quanto possa restare chiara da quello matematico [8] . Queste osservazioni di Hindemith mostrano che egli non è affatto disposto ad abbandonare un riferimento normativo alla pratica musicale - e questo gli può essere imputato come un merito o come un elemento di incongruenza metodica. Come un merito, perché sembra abbastanza giusto che l’astrazione teorica in questo campo non debba perdere di vista la concretezza dell’esperienza musicale; ma anche come una incongruenza metodica per il fatto che una esigenza stretta di non arbitrarietà richiederebbe l’esclusione di qualunque elemento normativo tratto dall’esperienza musicale. È certo in ogni caso che per Hindemith sono considerazioni musicali che determinano i limiti esterni del campo di azione del metodo e che, come vedremo, tendono anche a penetrare al suo interno ed a intevenire nella sua azione.
4. La procedura di spostamento di grado
La procedura di riduzione è dunque riconosciuta come impraticabile. E proprio la consapevolezza di questa impraticabilità, associata ad una inaudita ostinazione con cui viene perseguito il fine di una fondazione fisicalistica, che non si contenta dei risultati dei primi sei armonici e quindi di una mera giustificazione della triade maggiore e della tonalità nell’accezione tradizionale del termine, induce Hindemith ad escogitare una propria via per realizzarlo.
Come in una favola, egli dice [9] , immaginiamo di regredire ai tempi in cui le «note» non sono state ancora inventate e che si disponga soltanto del suono singolo e dei suoi armonici. - Come in una favola: postulando questo inizio immaginario Hindemith pensa forse di realizzare una sorta «epoché», di «messa in parentesi» delle conoscenze già acquisite, nello stile dei fenomenologi. Questa idea è certamente presente in Hindemith e viene ribadita nel volume Komponist in seiner Welt [10] quando ci si accinge ad introdurre la tematica del «materiale di lavoro». Si sottolinea allora che mentre i musicisti tendono a considerare questo materiale come qualcosa di dato, senza scorgere in esso alcun problema oppure a considerarlo sotto il profilo delle loro conoscenze apprese dalla scuola e dall’esercizio della loro professione, è necessario invece «indagare questo materiale e i suoi modi di applicazione come osservatori disinteressati, come farebbe un dilettante intelligente: non impediti dai paraocchi del musicista.. Noi procederemo come se dovessimo apprestare il materiale per il musicista - senza esperienza precedente, per così dire, dal nulla» [11]. E poco dopo sottolinea con insistenza: «Togliendo di mezzo i paraocchi del musicista, ci rendiamo liberi dai suoi vincoli al modo di pensare tradizionale, dalle sue preferenze personali, dai suoi binari stilistici e (questo è la cosa più importante) dalla sua difesa di tutto ciò di cui egli si è già appropriato attraverso l’esercizio, i suoi ragionamenti e riflessioni. In possesso di questa libertà noi possiamo considerare con occhi critici quei legami tradizionali e professionali. Forse potremo trovare addirittura dei metodi più convincenti e attendibili da applicare al materiale sonoro» [12]. Le espressioni qui ricorrenti - lo spettatore disinteressato, il paraocchi come immagine di conoscenze pregiudiziali che impediscono di cogliere la «cosa stessa», l’apprestamento di una situazione che ponga i problemi «senza esperienza precedenti, per così dire dal nulla» sono espressioni ricorrenti nella letteratura fenomenologica. Si tratta tuttavia di una epoché ben singolare, questa, che riporta, anziché, come dovrebbe, al mondo sonoro non ancora attraversato da apparati esplicativi, al suono singolo ed ai suoi armonici, che certamente sono un punto assai critico di passaggio dall’esperienza percettiva alla spiegazione fisica! Questa intenzione di regresso ad un ipotetico primo inizio resta tuttavia interessante per un fatto che è stato finora assai poco messo in evidenza dalla critica: essa fa tutt’uno con l’idea che questa attesa fondazione fisica ci metta nelle condizioni della tabula rasa facendo da preludio ad una radicale riformulazione dei concetti musicali di base.
Ma per il momento cerchiamo di sintetizzare la procedura proposta da Hindemith, che nella lettura del testo può presentarsi faticosa ed aperta a possibili equivoci.
Il suono singolo da cui prendiamo le mosse sia il do grave a 64 Hz [13] . La numerazione degli armonici comincia naturalmente di qui ed esso varrà quindi come primo armonico. Il secondo armonico presenta il do a 128 Hz. Data l’identità della nota, a parte la differenza di altezza, «essa potrà diventare suono fondamentale di una nuova serie di ipertoni che non mostrerà alcuna differenza rispetto alla prima, al di là della trasposizione di ottava. In virtù di questa proprietà, essa forma il limite superiore della nostra scala» [14]. Questo primo passo dello sviluppo degli armonici viene dunque interpretato come un passo che delimita uno spazio che dovrà essere via via riempito da nuovi suoni.
Il terzo armonico di do_64 - corrispondente a 64*3=192 Hz - non appartiene a questo spazio e non può essere accolto come tale. Tuttavia noi sappiamo già che il secondo armonico si trova in una relazione di ottava con il primo. Potremmo allora considerare il terzo armonico come secondo armonico di una fondamentale da ricercare. Questa verrà ottenuta dividendo la frequenza del terzo armonico per 2. Si ottiene allora un valore di 96 Hz, che è compreso tra 64 e 128 e che sarà dunque il primo intervallo con cui comincia l’articolazione dell’ottava di base. Si tratta di una quinta misurata dal rapporto di 3/2 (702 cents). Si noti che non si tratta per nulla - come si continua ripetere nelle esposizioni frettolose - di una procedura di riduzione all’interno dell’ottava nel senso in cui ne abbiamo parlato in precedenza, da farsi in ogni caso quando un armonico supera l’ambito dell’ottava di base. In questo caso la divisione per due è infatti determinata unicamente dalla decisione di considerare il terzo armonico come secondo di una fondamentale da ricercare.
«Con questo accertamento - sottolinea Hindemith - abbiamo in mano la chiave per tutti i calcoli sucessivi. Chi ha compreso il cammino or ora descritto da do_64 al di là di sol_192 verso sol_96 potrà seguire senza fatica l’origine del nostro sistema planetario dei suoni» [15].
In effetti se si è ben compreso il modo in cui avviene quel passaggio, si avverte anche subito la possibilità di una estensione procedurale. Potremo in altri termini interrogarci ad ogni grado, seguendo di passo in passo la serie degli armonici, se l’armonico in questione possa essere produttivo di una nuova nota all’interno dell’ottava di base qualora il suo ordine venga spostato e si ponga il problema della fondamentale corrispondente a questo spostamento. Ad esempio, in rapporto al quarto armonico do_256 ci si potrà chiedere che ne è della rispettiva fondamentale considerandolo come terzo e secondo. E si vede subito che come secondo armonico si ottiene come valore della fondamentale un valore già acquisito (128), mentre considerandolo come terzo armonico si ottiene un valore nuovo (256 : 3 = 85,33), compreso nell’ottava di base e che si trova in un rapporto di 4/3 con la fondamentale do_64 - una bella quarta a 498 cents. Di conseguenza questo valore verrà acquisito nel Tonleiter che stiamo costruendo. Naturalmente la giustificazione di questo intervallo starà tutta nell’esistenza nella serie degli armonici di una doppia ottava rispetto alla fondamentale, e non nell’esistenza effettiva di un intervallo di quarta. Ovvero: la doppia ottava è in grado di giustificare l’intervallo di quarta per il fatto che questo può essere calcolata da quella.
Potremmo chiamare questa procedura, differenziandola nettamente dalla precedente, «procedura di spostamento di grado».
Essa sembra possedere un automatismo sufficiente a porla al riparo dal problema dell’arbitrarietà delle selezioni. Infatti si possono formulare due regole per gli scarti da effettuare - regole che dovrebbero potersi caratterizzare come obbiettive, poggiando il loro utilizzo su criteri puramente numerici che potrebbero avere un’applicazione interamente automatica, senza che intervengano valutazioni mediate da un sistema musicale esistente.
Una nota verrà scartata
1. se si tratta di una nota già trovata
2. se la sua frequenza risulta superiore a 128, e quindi fuori dal margine superiore dell’ottava {64,128}. Se risulta inferiore a 64, e quindi fuori del margine inferiore dell’ottava, se ne farà il riporto all’interno di essa attraverso la moltiplicazione per due della frequenza e verrà esclusa se ricade nella prima regola.
Si vede subito tuttavia che nella formulazione della seconda regola vi è qualcosa che non convince. La prima non pone certamente alcun problema dal momento che si limita ad escludere i raddoppi. Ed anche le ragioni della seconda sarebbero altrettanto evidenti se stabilisse in generale l’esclusione di qualunque trasposizione, sia dall’alto che dal basso. Il metodo della riduzione entro l’ottava verrebbe così interamente bandito e al suo posto subentrerebbe il metodo dello spostamento di grado. Invece si stabilisce che la «riduzione entro l’ottava» sia consentita per le frequenze inferiori a 64. Naturalmente dal punto di vista strettamente calcolistico, si possono fissare le convenzioni che si vogliono: l’automatismo viene in ogni caso conservato e il criterio della selezione resta puramente aritmetico. Ma è certo lecito il sospetto che quella convenzione sia effettuata per prevenire un risultato indesiderato. Di fatto sembra difficile trovare nel testo osservazioni sufficienti per giustificare questa disparità.
4. Le tre fasi della deduzione della Serie 1
I.
Nell’illustrare la procedura, abbiamo già percorso un certo tratto della prima fase della deduzione della Serie 1. In effetti, abbiamo «dedotto», con riferimento ai primi quattro armonici, nell’ordine, l’ottava, la quinta e la quarta. Procedendo oltre, si passerà in esame il quinto armonico (che è un mi_320) e si otterrà, attraverso la procedura indicata e l’applicazione delle regole di selezione, un la_106,66, che è una sesta a 884 cents (5/3), e un mi_80, ovvero una terza a 386 cents (5/4) [16]. Si cominciano a dipanare gli intervalli considerati «giusti». La bontà del procedimento sembra ancora clamorosamente confermato dal sesto armonico (sol_384) che, considerato come quinto, esibisce un mi bemolle_76,8 che è una terza minore a 315,6 cents (6/5).
A questo punto le possibilità di derivazione legate direttamente ai primi sei armonici sembrano esaurite. A parte le considerazioni già compiute sul settimo armonico come tale, esso si rivela «improduttivo» qualora sia sottoposto alla procedura di spostamento di grado. Ciò significa che «se tentiamo di maneggiarlo così come abbiamo fatto con i suoi predecessori arriviamo a risultati terrificanti» [17]. Applicando quella procedura otteremmo dei risultati «calanti», che dovremmo includere nella partizione della nostra ottava perché non possono essere filtrati dalle due regole che abbiamo enunciato. Ciò significa peraltro che i risultati della procedura dello spostamento di grado applicata al settimo armonico sono altrettanto validi quanto lo sono quelli ottenuti nella sua applicazione agli armonici precedenti. Intervengono invece considerazioni estranee al calcolo per confermare l’opportunità di arrestarsi al sesto armonico. E naturalmente si contravviene all’assunzione di essere prima di ogni sapere musicale, «come in una favola». Se quell’assunzione fosse rigorosamente mantenuta continueremmo la deduzione proseguendo i calcoli sul settimo armonico e oltre. Allora si prospetterebbe certamente la situazione che si prospetta nella procedura di riduzione semplice degli armonici all’ottava di base - ovvero il progressivo riempimento completo di essa, il venire meno della sua «discretezza» e la perdita di senso del problema della partizione ed a maggior ragione della sua legittimità. Ci si deve dunque arrestare di fronte al settimo armonico: qui comincia il caos, e su questa frontiera del numero sette si fa avanti anche la tentazione numerologica: «Nell’antichità i numeri e le relazioni numeriche dicevano di più di quanto dicano agli uomini di oggi che hanno dimenticato il senso segreto del numero per via della loro familiarità con liste di prezzi, statistiche e bilanci. Il segreto del numero sette era ben noto: chi fosse riuscito a impadronirsene sarebbe potuto diventare signore del mondo o suo distruttore. È comprensibile che un simile numero mistico e inafferrabile fosse considerato sacro. Ed anche per la sensibilità ai suoni il sacro recinto è inaccessibile» [18].
È dunque definitivamente deciso che occorre limitare la procedura proposta ai primi sei armonici sviluppandola eventualmente a partire dai suoni che attraverso di essi vengono prodotti. In effetti vi sono due possibilità di estensione del metodo di spostamento di grado che consentono di proseguire nella deduzione. Se è lecito considerare questo spostamento verso il basso dovrebbe essere altrettanto lecito riferirlo anche ai gradi superiore della nota considerata. Cosicché si potrà cominciare dal terzo armonico [19] considerandolo come se fosse quarto, quinto e sesto armonico, proseguendo poi con il quarto (considerato come quinto e sesto) e con il quinto (considerato come sesto). I calcoli mostrano che, rispettando le nostre due regole di selezione, da questa estensione della procedura possiamo acquisire solo una nuova nota: dal quarto armonico, do_256, considerato come quinto, possiamo trarre il la bem_102,4, e quindi un nuovo intervallo pari 813.704 cents(8/5).
Con questo passo viene considerata chiusa la prima fase di costruzione della serie che ci ha portato alla seguente sequenza:

II.
Abbiamo accennato ad una seconda possibilità di proseguire la successione. Il suo impiego dà luogo alla seconda fase della deduzione: avendo esaurito tutti i calcoli possibili entro il sesto armonico a partire dalla frequenza do_64, sembra coerente utilizzare come frequenza di base ciascun suono precedentemente prodotto considerato nell’ordine. «La forza produttiva del suono origine do_64 si è esaurita. I suoni che sono nati da esso do_128, sol_96, fa_85,33 la_106,66, mi_80, mi bem_76,8, la bem_102,4 lo circondano come un numero orgoglioso di figli. Essi cominceranno un giorno una vita indipendente quando essi avranno abbandonato la casa del padre - questo processo nella famiglia dei suoni si chiama modulazione. Essi possono tuttavia fondare la loro propria famiglia quando si trovano ancora sotto la protezione paterna e possono rallegrare il loro genitore con una frotta di nipoti. Per noi ciò significa che possiamo trattare gli armonici dei suoni da Sol_ 96 a la bem_ 102,4, in quanto si trovano nella cerchia dei primi sei armonici di C_64, così come abbiamo fatto per questi ultimi» [20]. Come si vede, si cerca di motivare questo passaggio con un riferimento musicale, la modulazione: se chiamiamo tonica il suono generatore della serie, possiamo dire che ogni suono può assumere carattere di tonica e generare la propria serie; ma può anche assumere il carattere di tonica subordinata, generando i propri figli «quando si trova ancora sotto la protezione del padre». Del resto lo stesso metodo di spostamento di grado potrebbe in qualche modo essere giustificato con il fatto che una stessa nota può essere indifferentemente, secondo i contesti e le funzioni, quinta, terza, quarta ecc. di una tonica da determinare. Analogie, è appena il caso di dirlo, arrischiatissime dove si gioca proprio su un ambiguo intreccio tra livello fisico e livello musicale ed indicative soltanto di una direzione complessiva del discorso verso un tentativo di ridiscussione del concetto di tonalità a partire dal suo radicamento dentro la struttura fisica del suono. In realtà, l’unica giustificazione possibile di questo passaggio è di carattere matematico-formale, e riguarda il fatto che poiché i valori precedenti sono stati ottenuti attraverso un calcolo, si può ammettere che essi possano rappresentare basi per applicazioni dello stesso tipo di calcolo, preservando l’unità del processo.
Procedendo in questo modo, si cercheranno dunque nuovi valori cominciando a prendere il terzo armonico di sol_96, e effettuando lo spostamento di grado sia sopra che sotto di esso. Proseguendo poi consequenzialmente. Il numero dei calcoli cresce, ma la procedura resta nell’essenziale la stessa. Non è il caso di tediare il lettore riproducendola passo per passo, ma possiamo limitarci a riferirne i risultati. A partire da sol_96 si ottiene un re_72 (ovvero un tono grande o pitagorico a 204 cents, 9/8). Considerando gli armonici di fa, possiamo acquisire un si bem_113,78 (996 cents, 16/9) ed un re bem _68,27 (112 cents, 16/15); attraverso gli armonici di mi si ottiene un si_120 che è pari a 1088 cents ovvero al rapporto 15/8..
Così la serie che stiamo sviluppando si arricchisce dei nuovi valori indicati dopo la seconda doppia barretta:

Ma questa volta, in questa seconda fase della deduzione, le cose non sono andate così liscie come erano andate nella prima. In effetti nella prima fase tutti i valori erano stati ottenuti o rifiutati in stretta osservanza delle due regole.Ora invece è accaduto che nel corso della procedura alcuni valori siano stati rifiutati sulla base di considerazioni del tutto estranee alla procedura calcolistica. In sostanza accade che si ottengano, esattamente come nel caso della derivazione dal settimo armonico, intervalli troppo piccoli rispetto a quelli già ottenuti, cosicché vengono scartati dei valori, perfettamente legittimi dal punto di vista calcolistico, ma «non adatti al nostro scopo» [21].
III.
Questa situazione si aggrava nell’ultima fase della derivazione. Nella prima fase abbiamo derivato nuovi valori prendendo come base dei calcoli i primi sei armonici di do_64, con spostamento di grado sotto e sopra. I primi sei armonici, per impiegare la metafora hindemithiana, possono essere considerati i «figli» di do_64. Nella seconda fase le note generatrici sono proprio questi «figli» e le note da esse generate possono dunque essere dette «nipoti». Ora, osserva Hindemith, «i figli di do_64 hanno fatto il loro dovere, e tuttavia la nostra scala non è completa. Se ordiniamo in ordine crescente le note finora ottenute tra do_64 e il suo secondo armonico do_128, tra fa_85,33 e sol_96 si apre una lacuna» [22]. Fra queste due note sussiste un intervallo più ampio di quello che sussiste tra le altre note. In sostanza dobbiamo ancora «dedurre» il tritono e la via più ovvia per farlo, ad imitazione del passaggio dalla prima alla seconda fase, è quella di passare ad una terza fase che consisterà nell’assumere come base dei calcoli i «nipoti» e nell’applicare la procedura di spostamento di grado agli armonici di essi. Ma questa deduzione risulta assai più controversa: valori falsi, ma calcolisticamente validi, spuntano da ogni parte, in particolare ricreando proprio quegli intervalli minimi che erano generati dal settimo armonico. Non è un caso se in questa fase Hindemith evita una ricerca sistematica limitandosi a individuare un valore «passabilmente» intermedio tra fa_85,33 e sol_96. Ma questa ricerca non va a buon fine: in effetti ci veniamo a trovare di fronte a tre valori molto vicini tra loro compresi tra 85,33 e 96 Hz: 92,16 Hz (pari a 631), 91 Hz (pari a 609 cents) e 90 Hz (pari a 590 cents). Più esattamente: il primo era già stato trovato nella fase precedente e scartato perché se ne sarebbe potuto trovare un altro migliore, essendo questo troppo alto! [23] In questa situazione non vi è che l’arbitrio, che tien d’occhio la prassi musicale, che può prendere qualche decisione. Hindemith decide di accettare in via di principio entrambi i due valori 91 e 90 a titolo rispettivamente di sol bemolle e fa diesis e di fatto optando per il valore 90 come fa diesis. In via di principio la differenza deve essere mantenuta per il fatto tra l’uno e l’altro valore, separati da solo 1 Hz, intercorrono in questa regione di frequenza circa venti cents - un divario chiaramente percepibile. Proprio al termine della deduzione - mentre abbiamo incontrato già in precedenza situazioni di difficoltà risolte alla bell’e meglio - dobbiamo prendere atto di questa situazione piuttosto imbarazzante.
«A quanto pare nell’intervallo tra fa diesis e sol bemolle abbiamo riottenuto ciò che volevamo evitare nel calcolo del settimo armonico. Ciò vale tuttavia soltanto per questa singola nota, le note della scala finora ottenute non vengono toccate da ciò. Con questo piccolo disturbo possiamo arrivare alla fine; al «crepuscolo degli dei» dei suoni che sarebbe subentrato se avessimo incluso il funesto settimo armonico, non avremmo potuto opporre difesa. Nella nostra posizione (l’ottava grave) il comma misurato dalla grandezza di una oscillazione, è tuttavia ancora così grande che l’orecchio percepisce la differenza. Essa è comunque pur sempre la più piccola percepibile e in ogni caso più accettabile che quella che sarebbe sorta dall’inserimento di un sol bemolle a 92.16 derivato dal mi bemolle» [24].
Naturalmente, dal punto di vista matematico nulla osta a proseguire oltre con i pronipoti - ma « poiché già i pronipoti sono affetti dalla tensione del comma, tutti i suoni da essi derivati peggiorerebbero quanto a purezza e perderebbero la connessione armonica con il suono originario. Per giunta la nostra scala è completa e noi non abbiamo bisogno di alcuna altra nota» [25].

Riordinata scalarmente la Serie 1 esibisce le dodici note della «scala cromatica». Si noti che la scelta dell’impiego del bemolle o del diesis è in questo contesto pura convenzione. Si tratta anzi di un impiego equivoco, non essendovi alcuna idea di innalzamento o di abbassamento - gli armonici sono esattamente quello che sono. Oltre che le distanze dalla nota iniziale vengono qui indicati, nella riga inferiore, i tipi di intervalli che intercorrono tra l’una e l’altra posizione.
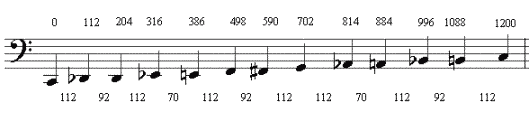
Come si vede, vi sono tre tipi di intervalli semitonali, un semitono piccolo a 70 cents, medio a 92 cents e grande a 112 cents. In realtà si tratta di misure ben note nella tradizione europea. In rapporti: 70 cents = 25/24; 92 cents = 135/128; 112 cents = 16/15. Come differenza tra 92 e 70 si ottiene il comma sintonico (81/80) a 22 cents. Poiché questi sono i numeri è facile scorgere sopra questa scala cromatica, la scala diatonica zarliniana:

Non è difficile pensare che questo modello pesi nel corso della deduzione della serie 1 [26] .
6. La soppressione del fisicalismo
Nelle considerazioni precedenti è già stato fatto valere come elemento di critica il fatto che il metodo proposto non viene ovunque coerentemente seguito, e ciò significa che nel corso della «deduzione» intervengono scelte che appaiono giustificate al di fuori di esso. Non solo l’obiettivo da raggiungere è predelineato, ma si fanno valere opzioni al solo scopo di non mancarlo. All’automatismo subentra un elemento di arbitrarietà. La «messa in parentesi» della normatività di modelli conosciuti non viene rispettata con il necessario rigore. Solo tenendo d’occhio la pratica musicale e partizioni ben note dell’ottava possiamo precluderci di continuare a dedurre anche dal settimo armonico ed oltre; ed è sempre questa stessa pratica che suggerisce di non acquisire valori che sono stati, nel senso che abbiamo spiegato, legittimamente dedotti, oppure di operare delle scelte tra valori intervallari troppo vicini. Questi argomenti sono del resto correntemente usati nelle critiche della posizione di Hindemith. Io credo tuttavia che per comprendere che cosa veramente accade in questa deduzione sia più interessante, riportare l’attenzione più a monte, e quindi sulla procedura dello spostamento di grado e sulla ricerca di una «posizione» attraverso l’identificazione della fondamentale del grado che è stato spostato. Questa procedura è in realtà assai imbarazzante proprio in rapporto ad una tesi forte delle radici fisiche della partizione.
Riflettiamo su questo punto. Gli armonici di un suono sono un fatto fisico concreto, e persino entro certi limiti, nella regione più prossima al suono-origine, un fatto fisico che arriva ad una manifestazione fenomenologica. In circostanze particolari favorevoli, l’armonico lo si sente effettivamente risuonare dentro il suono più grave. Ed è questo punto - l’immanenza effettiva degli armonici nel suono singolo - che è sempre stato il motivo principale del fascino teorico che essi hanno da sempre così fortemente esercitato. Ora, proprio questo punto viene in questo caso del tutto a cadere. Nel metodo proposto da Hindemith, ciò che importa non è il fatto di ritrovare concretamente l’armonico dentro il suono. Questo è anzi in linea di principio escluso. Se si considera il quarto armonico di un suono A come terzo o quinto armonico di un altro suono B e si trova significativo proprio questo suono B in rapporto ad A, si deve certo dare per scontato che il suono B non ha nessun rapporto fisico con A e tanto meno avremmo ragione di dire che è contenuto in esso. Sembrerebbe quasi un paradosso che si cerchi la giustificazione di un rapporto relativamente ad una fondamentale nei suoi armonici considerati come armonici di un’altra fondamentale! Questo paradosso viene tuttavia meno se si considera che la condizione richiesta è unicamente la derivabilità calcolistica, la calcolabilità del suono B a partire da un armonico di A. Occorre avere chiaramente presente che ciò che si cerca non è una entità in qualche modo concreta, ma niente altro che un numero per il quale si richiedesoltanto che sia derivabile da altri numeri secondo un unico metodo che riporta tutti i risultati ad una base comune: 64 rappresenta l’inizio, i numeri da 1 a 6 fungono da moltiplicatori (per raggiungere gli armonici) e da divisori (per raggiungere le fondamentali corrispondenti). In fin dei conti è soltanto quel 64 e l’ostinato richiamo agli Hz che ci ricorda il riferimento alla frequenza [27] .
Peraltro Hindemith non si è reso conto che questo riferimento, nella sua procedura, potrebbe essere neutralizzato a tutto vantaggio, tra l’altro, della chiarezza del risultato e della semplificazione dei calcoli. Il lettore è infatti di continuo portato a chiedersi, mentre è costretto a far di conto, se non vi sia una qualche via per liberarsi di questo impiego dei valori assoluti essendo lo scopo quello di raggiungere dei rapporti intervallari del tutto indipendenti da essi. Di fatto questi calcoli in Hz sono alquanto fastidiosi e in ultima analisi non appropriati alla natura del problema proposto.
Ora, a ben pensarci, vi è un modo per operare solo con rapporti, sia pure utilizzando un piccolo trucco: poiché il numero di base in via di principio può essere qualsivoglia, è sufficiente scegliere per esso il numero 1 perché l’aspetto fisico risulti del tutto neutralizzato di fronte a quello matematico-calcolistico. In tal caso infatti la serie degli armonici, compresa la fondamentale, risulterebbe costituita dai numeri da 1 a 6 e tutto verrebbe costruito con essi. Il vantaggio di ciò consisterebbe nel fatto che l’operazione di divisione richiesta per ottenere la fondamentale ricercata nello spostamento di grado non avrebbe bisogno di essere eseguita e rappresenterebbe di per se stessa, presentata in forma frazionaria, la misura matematica degli intervalli. Ad esempio: il terzo armonico della frequenza di base 1 è rappresentato dal numero 3. Ma se questo viene inteso come secondo armonico, allora esso andrà diviso per 2. Ora, 3/2 può essere già considerato il rapporto intervallare da acquisire. Così parlare di quarto armonico considerato come terzo significa niente altro che proporre già l’intervallo di quarta (4/3).
Nel caso della seconda e della terza fase della procedura, ovviamente, si assumerà, come base, ottenuto nella prima o, rispettivamente, nella seconda fase. E si proseguirà coerentemente, mettendo in opera le regole di selezione opportunamente riformulate. In questo modo si otterrebbero i risultati ottenuti da Hindemith in modo assai più agevole, più generale ed elegante.
I Fase

I numeri da 1 a 6 in verticale indicano gli armonici (oppure, se si preferisce, i moltiplicatori della frequenza di base), in orizzontale rappresentano i divisori. Così il 5/4 presente in tabella rappresenta l’intervallo di terza maggiore ottenuto attraverso il quinto armonico considerato come quarto. La tabella potrebbe essere completamente (e agevolmente) riempita dai valori corrispondenti, facendo agire poi le regole di selezione. La seconda fase richiede una rappresentazione leggermente più complicata, perché debbono essere indicati i valori già acquisiti, cosa che si può fare come è mostrato dalla tabella seguente. In essa, sulla sinistra si leggono gli armonici corrispondenti - ad es. 9/2 come terzo armonico di 3/2; sulla destra invece i valori acquisiti attraverso lo spostamento di grado - ad es. 9/8 come risultato della divisione di 9/2 per 4 (terzo armonico di 3/2 considerato come quarto)
II fase
Analogamente per la terza fase, che porta all’acquisizione di due valori, di cui uno viene comuque «scartato».
III fase

Naturalmente per ottenere i valori in frequenza di Hindemith basterà moltiplicare 64 per i rapporti ottenuti. Ma il punto interessante è che con questo metodo di presentazione risulta con un’evidenza che salta agli occhi il fatto che l’elemento fisico si è volatilizzato. Il fisicalismo di Hindemith è un fisicalismo che si autosopprime. È invece il «senario» che celebra qui un proprio estremo e tardivo trionfo: il primo piano è ora tutto occupato dal «numero sonoro», è soprattutto dall’antica teoria dei rapporti semplici come quelli che garantiscono in via di principio gli intervalli «migliori».
7. La nozione di affinità tonale
C’è chi ha scritto che la costruzione di Hindemith sugli armonici è una pura mostruosità [28]. Ma credo che si debba intanto ammettere che la procedura è ingegnosa e il risultato della sua applicazione potrebbe apparire persino stupefacente. Perché non cedere ad un primo entusiasmo provvisorio, dimenticandoci per un attimo le obiezioni che abbiamo già tracciato per via ed in particolare le ultime considerazioni che ci fanno apparire le cose sotto una luce ben diversa? Un veritable monstre, in effetti, una vera meraviglia! Accade infatti che, nel nostro andirivieni tra gli armonici, salendo e discendendo di grado, non solo abbiamo cavato i dodici suoni della «scala cromatica», ma assume un significato peculiare addirittura l’ordine in cui ogni suono è stato ottenuto, esprimendo quello che Hindemith chiama il grado di affinità tonale (Tonverwandschaft) di ogni suono con il suono generatore. Così egli scrive sottolineando vivacemente questo punto:
«La successione nella quale i suoni della scala entrano nel mondo sonoro a partire dal suono che li ha prodotti, ha la massima importanza per la concezione presentata in questo libro. Essa non dimostra soltanto che i suoni appartengono ad una famiglia, appartenenza che si manifesta nel legame con il suono principale, ma essa presenta soprattutto una lista d’ordine inequivoca delle affinità tonali. Essa dice: una certa nota e quella che risuona una ottava più in alto stanno in un rapporto di affinità così stretto che non si può quasi tra esse rilevare una differenza. Dopo l’ottava, la nota più acuta di una quinta è l’affine più prossimo, e poi seguono note che si trovano dalla nota fondamentale (Grundton) a distanza di una quarta, di una sesta maggiore, di una terza maggiore, di una terza minore e così via. Questa misura del valore delle affinità ha una validità incondizionata. Ogni volta che dei suoni vengono messi insieme debbono esserci sempre dei suoni che dominano sugli altri e suoni che sottostanno ad essi. Per quanto la loro sovranità possa estendersi per lunghi tratti oppure durare solo poche pulsazioni, in ogni caso ad essi si associano sempre i loro compagni secondo l’ordine di valore depositato nella serie dei gradi decrescenti di affinità» [29].
Inoltre Hindemith tiene a sottolineare che la questione non dipende da fatti di ordine linguistico (questione di stile, egli dice) e che essa appartiene alle basi elementari della musica stessa:
«Nel campo delle relazioni tra i suoni non valgono questioni di stile e neppure può esservi progresso, esattamente come non possono esservi questioni di stile nella tavola pitagorica e progresso nelle leggi più semplici della meccanica» [30].
E tuttavia... Vogliamo prendere per buona tutta la deduzione di Hindemith - in ultima analisi il giudizio non va dato solo sulla perfezione o le imperfezioni dei conteggi, ma sui problemi che in qualche modo vengono sollevati e per le motivazioni che stanno alla loro base, per i concetti a cui si cerca di dare un profilo. Qui in particolare abbiamo a che fare con questa nozione di affinità tonale. Possiamo essere certi di aver compreso con chiarezza di che si tratta? O meglio: al di là del metodo della deduzione che fornisce una determinazione astratta del rapporto con lo Stammton - con il suono generatore - ci dobbiamo chiedere in che cosa consista questa nozione di «affinità» dal punto di vista percettivo. Deve infatti trattarsi di qualcosa che si può udire, come una sorta di distanza avvertibile indipendentemente dalla conoscenza del sussistere di un’effettiva possibilità di derivazione.
Naturalmente si comprendono molto bene le intenzioni che stanno alla base della sua teorizzazione. La tematica dei gradi di affinità contiene l’idea del mondo sonoro come un mondo che ha un centro ed una periferia, e quindi un ordine intrinseco, una relazionalità interna. In essa è contenuta l’immagine di un «sistema planetario» [31]- un sole centrale con i suoi pianeti - che è anche nello stesso tempo un’immagine di armonia che rimanda dal mondo dei suoni al mondo stesso: oltre che un’immagine di unità, che diventa realmente molto forte se i pianeti vengono intesi come emanazioni del sole stesso.
Particolarmente indicativa è da questo punto di vista la rappresentazione della Serie 1 che viene proposta una volta anche torcendo il rigo in una spirale, dove la spirale è utilizzata non tanto per indicare una proseguibilità della serie, che viene anzi respinta, quanto piuttosto per indicare che la distanza dal centro aumenta progressivamente:

Ma con tutto ciò resta la nostra domanda. Vi è qualcosa che riempie, nella percezione del suono, questa nozione di affinità? Hindemith di ciò non parla affatto. Se dovessimo andare alla ricerca di una risposta per conto nostro certamente saremmo tentati di richiamarci al problema della consonanza e la dissonanza. Proprio in rapporto al primo passo della serie si rileva che «una certa nota e quella che risuona una ottava superiore stanno in un rapporto di affinità così stretto che non si può quasi tra esse rilevare una differenza» [32]. Sembrerebbe allora giustificato l’assumere questo rapporto come una sorta di modello per rendersi conto del significato concreto dell’affinità. Se poi si esamina la serie, rispetto al suono di provenienza, le note successive sembrano presentarsi bene o male in un ordine di dissonanza crescente. Se consideriamo le cose sotto questa angolatura non mancano nessi ed analogie di ordinamenti con le «scale di consonanza» della trattatistica del passato [33] . Ma vi è più di una ragione che ci impedisce di avviarci in questa direzione.
In primo luogo deve essere notato quanto poco, nel testo di Hindemith venga impiegati termini come consonanza e dissonanza. Essi non si incontrano in tutta l’esposizione della Serie 1. E se ne possono comprendere le ragioni. L’idea della relazionalità interna del mondo sonoro, del suo ordine immanente ha un evidente risvolto positivo e un altrettanto evidente risvolto polemico. Si tratta, come progetto positivo, di avviare un ripensamento sulla nozione di «tonalità» che tende, non già alla ripresa pura e semplice del linguaggio tonale, ma ad una generalizzazione della nozione che superi la particolarità di quel linguaggio ponendosi, almeno in via di principio, al livello del materiale dei linguaggi della musica. Dal punto di vista polemico vi è certamente la critica di tutte quelle tendenze che fanno dell’arte del comporre un pura questione di esercizio del libero arbitrio, nel completo misconoscimento dell’esistenza di strutture relazionali immanenti al suono stesso:
«A tal punto la sensibilità naturale si è oggi intorbidata che modi di comporre che fanno conto sull’assoluta mancanza di relazioni dei suoni tra loro possono diventare di moda! A nessun falegname verrebbe in mente di non prestare attenzione alle proprietà del suo legname da costruzione e di incollarlo per diritto e per traverso senza riguardo alla sua struttura. L’unica giustificazione di questi nuovi tentativi sta nell’orecchio che, nella sua struttura raffinatissima, è tuttavia ancora tanto robusto che, rispetto a complessi sonori messi insieme senza istinto ed a caso, non si comporta in modo da rifiutarli con tanta forza quanta ne metterebbero vista e tatto di fronte ad una sedia miserabilmente messa insieme» [34].
Ora il problema è: volendo condurre questa critica a fondo, è possibile servirsi della distinzione grezza tra consonanza e dissonanza così come si propone sul piano percettivo? In realtà questa distinzione potrebbe non essere lasciata agli incidenti di ordine storico ed alla particolarità psicologiche qualora fosse riconsiderata ed elaborata alla luce di una impostazione fenomenologica. Ma questa via è fondamentalmente estranea all’ambito del discorso hindemithiano, anche se non si può negare che esso sia attraversato da spunti significativi anche in questa direzione. Per ciò che concerne la distinzione tra consonanza e dissonanza Hindemith pensa certamente che, servendosi di essa, si presterebbe il fianco a critiche che avrebbero buon gioco nel sottolineare che una simile distinzione è esposta ad ogni possibile controversia. Inoltre la sua utilizzazione potrebbe far pensare alle antiche remore sull’impiego della dissonanza che sono, anche dal punto di vista di Hindemith, da respingere. Egli stesso, quando ne parla prudentemente, rievoca i consueti argomenti contro la portata di questa distinzione:
«Quesi concetti hanno mai ricevuto un chiarimento completo, nel corso di un millennio le definizioni sono cambiate: prima le terze erano dissonanti, più tardi divennero consonanze; si distinse tra consonante perfette e imperfette; attraverso un uso massiccio dell’accordo di settima, alle nostre orecchie la seconda maggiore e la settima minore sono quasi diventate consonanze; la posizione della quarta non mai stata chiarita in modo univoco; i teorici a partire da fenomeni acustici sono pervenuti più volte a spiegazioni interamente diverse da quelle dei musicisti pratici» [35].
Da un lato dunque è necessario fare un impiego assai parco di questa stessa terminologia, dall’altro rimettersi invece, per quanto riguardo le tematica ad essa sottesa, al punto di vista «fisicalistico» che sembra essere l’unica via che consente determinazioni oggettive. Questa tematica non è tuttavia contenuta nella Serie 1, ma piuttosto nella Serie 2, come viene esplicitamente sottolineato [36] .
Serie 2

Ed anche a proposito di quest’ultima Hindemith sottolinea che pur essendo qui presente il problema della distinzione tra consonanza e dissonanza, la serie, considerata da questo punto di vista non indica alcun luogo preciso in cui l’una nozione si contraddistingua dall’altra, potendosi far valere queste designazioni con certezza solo sui limiti estremi - intervallo di ottava e di settima. «I suoni consonanti sarebbero di conseguenza localizzati sul lato sinistro della serie 2, le dissonanze sul lato destro. In quale grado tuttavia la consonanza venga meno negli intervalli disposti a sinistra e la dissonanza cresca sulla destra non è accertabile con dei dispositivi di misura» [37]. Si cercano inoltre degli altri termini da sostituire a quelli di Konsonanz e di Dissonanz - ad esempio si parla, in questo stesso contesto, di Wohlklang e di Missklang. Si noti di passaggio che il tritono «non può essere ordinato nè nella regione del Wohlklang né essere considerato come Missklang; esso sta anche in questo caso nuovamente a parte come intervallo particolarissimo» [38].
Come abbiamo già rapidamente osservato, la Serie 2 ha una origine ed una costruzione interamente diversa dal punto di vista fisico, facendo riferimento ai suoni di combinazione. Il risultato è tuttavia innegabilmente simile - per quanto riguarda la pura forma della successione - alla Serie 1, se si sceglie un’unica nota come nota di riferimento.

Come si vede l’unica differenza riguarda gli intervalli di terza e di sesta che ricevono una diversa collocazione nella successione. Tuttavia Hindemith giustamente ribadisce la netta differenza, che è da ricercare sia nel modo della costruzione delle due serie, sia nel loro significato che non è affatto leggibile dalla pura e semplice presentazione grafica delle due serie. Nel primo caso, viene indicata la relazione di «affinità» rispetto ad un’unica nota assunta come nota «generatrice». Nel secondo caso invece abbiamo uno studio degli intervalli come tali - e la distribuzione dell’ordine avviene sulla base di considerazioni riguardanti la posizione che assume il suono fondamentale (Grundton) dell’intervallo stesso, secondo una nozione di suono fondamentale che è una creazione originale di Hindemith e che ha una importanza decisiva per comprendere la sua idea di «tonalità». L’impiego di una unica nota di riferimento non è qui rilevante, perché è rilevante soltanto il tipo di intervallo. Per riprendere la metafora del sistema planetario: in precedenza si considerava l’organizzazione dei pianeti rispetto al sole, ora si considerano i rapporti dei pianeti tra loro.
Resta infine da notare che se considerassimo la Serie 1 sotto il profilo del problema della consonanza e della dissonanza verremmo a rimetterci proprio l’elemento della «filiazione» che rappresenta il punto su cui è giocata tutta la sua costruzione. Ma questa conclusione ci riporta alla domanda iniziale. Ci siamo chiesti infatti se questa nozione di affinità tonale avesse un qualche «corrispondente intuitivo»: e le nostre precedenti considerazioni ci lasciano senza aiuto, non sappiamo né come né dove possiamo cercarlo e trovarlo. Vi è forse qualcosa di simile ad un volto delle note nel quale possiamo scorgere la somiglianza con il padre o qualcosa di simile ad un’aria di famiglia? Se non possiamo contare per stabilire queste somiglianze sulla relazione di consonanza e di dissonanza e se dobbiamo strettamente mantenere l’idea della «filiazione», sembra proprio che questo concetto di affinità debba restare un concetto vuoto, ovvero affidato unicamente alla procedura di deduzione dagli armonici nei termini in cui è stata descritta. La nozione di relazione tonale, concepita così, minaccia in tal caso di appartenere più al regno del pensiero che a quello delle strutture musicali concrete. Credo che Hindemith avverta questo problema ed anzi se ne assuma la responsabilità quando è indotto ad una singolare riflessione che associa le idee che stanno alla base della Serie 1 alla musica mundana, all’armonia delle sfere che non può essere udita da orecchie umane e la cui traduzione in percezioni concrete potrebbe apparire come una degradazione ed una profanazione:
«Un unico suono come radice della scala corrispondente, la serie dei dodici suoni cromaticamente ordinata nata dalle tensioni che sorgono attraverso la contrapposizione di unità vibranti in rapporti di grandezza dei numeri semplici da 1 a 6 - non suona tutto ciò come una sommessa eco della musica mundana degli antichi, di quelle armonie delle sfere che troneggiava sopra gli altri due tipi di musica terrestri - la musica humana e quella «quae in quibusdam constituta est instrumentis»? Quelle armonie sono così perfette che gli organi di senso insufficienti degli uomini non le percepivano, ed anzi esse non avevano bisogno di una realizzazione attraverso i suoni, poiché i rapporti numerici come fondamento e senso di ogni movimento e di ogni suono sono, per lo spirito pensante, qualcosa di più che l’elemento esteriore della musica, il suono, attraverso il quale esse sarebbero profanate e riportate dentro la sfera umana del percepibile. Una differenza essenziale tra musica humana e instrumentalis non sussiste oggi più per noi grazie alla conoscenza del loro fondamento fisico comune, ed anche tra musica mundana e humana oggi possiamo prestare attenzione più a ciò che hanno in comune che a ciò che le distingue. Noi non faremmo come facevano gli antichi, che proiettavano i rapporti terrestri nello spazio cosmico, ma sentiamo estendersi fino nelle più minute particelle costruttive musicali forze che sono le stesse di quelle che mantengono in movimento il cielo fino alle nebulose più lontane» [39].
Si tratta di una citazione assai caratteristica dell’atteggiamento e dell’atmosfera che circonda l’impresa di Hindemith: essa non ci illumina solo su ciò che sta sullo sfondo, ma indica anche che, in ultima analisi, la Serie 1, mantiene un carattere di oggetto mentale piuttosto che di una realtà musicale concreta.
Tutto ciò fa riflettere sulla nozione di tonalità qui in gioco. Saremmo tentati di dire che la decisione di non passare attraverso la nozione di consonanza per la costituzione del concetto è una decisione presa, in realtà, a ragion veduta. Infatti, scegliendo quella via non si potrebbe arrivare a stabilire una nozione di tonalità tanto forte come quella a cui Hindemith pretende di dare fondazione. Le nozioni di consonanza e di dissonanza non contengono affatto quella di tonalità, anche se si potrebbe sostenere che la nozione di tonalità possa essere posta attraverso di esse. Facendo uso di determinate regole, il gioco delle consonanze e dissonanze, insieme certo ad altri elementi, «pone in essere» un centro tonale, «fa esistere» tonica, dominante, sottodominante e tutto il resto. Ma se questo è vero, allora la nozione di tonalità non può essere sottratta al livello linguistico, mentre è proprio questo che si pretende di fare nella forma che il problema assume in Hindemith. Stando alla sua posizione si deve poter parlare di relazioni tonali in un senso tale da poter essere riferito al «materiale di lavoro», che rappresenta un livello indipendente rispetto grammatiche musicali particolari e precisamente il livello con cui ogni grammatica non può che avere a che fare.
L’idea della «filiazione» ha esattamente questo senso e questa portata, e il suo scopo è quello di sottrarre la nozione di tonalità dal livello fenomenologico - perché a partire di qui non si potrebbe fare altro che rendere più evidente la sua appartenenza al piano dell’elaborazione linguistica del materiale - tentando di riportarla ad un livello prelinguistico che qui non può che significare altro che il livello di considerazioni fisicalistiche.
Ma allora le osservazioni che abbiamo compiuto per la Serie 1 e per l’idea di affinità tonale che viene teorizzata sulla sua base si riflettono ovviamente sulla nozione di tonalità.
Leggiamo dopo queste considerazioni il passo seguente:
«La forza dell’affinità che promana da un tono fondamentale comune e che costringe insieme gli intervalli di tutte le grandezze e specie, che regola il corso dei suoni senza che essa debba venire necessariamente udita, non è essenzialmente eguale né alla forza armonica né a quella melodica, che agisce nelle connessioni tra le note, e nemmeno essa è da intendere come una somma di tutte le tensioni che sono richiamate da queste forze - benché spesso essa sia scambiata in particolare con la forza armonica e di fatto esso può essere scambiata facilmente con essa. Sopra tutte le altre forze domina la forza del tono fondamentale comune, in tutti i decorsi sonori si avverte l’azione di un fermento segreto, nascosto: quello del legame tonale. Esso è ovunque presente a tal punto che non ci riuscirà mai di reprimerlo. Noi potremo trovare delle successioni di note nelle quali esso appare respinto, potremo nasconderlo, applicarlo in modo falso o bistrattarlo, ma non potremo dissolverlo. Se riusciamo a renderlo inavvertibile in un luogo, esso eserciterà tanto più fortemente il suo dominio in un altro. Per quanto possiamo volare in alto con palloni o aereoplani e dire a noi stessi di volar via dalla terra, tuttavia la forza dell’attrazione terrestre ci costringe sempre di nuovo al suolo. La forza del legame tonale non è altro che la forza di gravità nella sua forma più raffinata» [40].
Quello che ci colpisce di più in questa frase non è tanto l’analogia conclusiva con la forza di gravità, in cui il naturalismo di Hindemith fa sentire tutto il suo peso, quanto l’inciso secondo il quale la forza della affinità (parentela) che promana da un tono fondamentale non ha bisogno di essere realmente udita. L’errore di considerare il tono fondamentale una origine piuttosto che un risultato è qui compiuto in modo realmente esemplare. E nello stesso tempo si accetta di pagare lo scotto di una possibile tonalità nascosta. Essa naturalmente può essere manifesta e comparire in primo piano:
«Tutti i suoni di questa serie, in qualunque modo possano susseguirsi gli uni agli altri, vengono sempre riferiti dall’orecchio al suono dominante principale do, nella misura in cui gli si dà l’occasione di far sentire la sua forza vincolante. Noi non udiamo più soltanto intervalli e accordi, ma abbiamo la sensazione di una sorta di forza magnetica che stabilisce un orientamento secondo un punto medio comune» [41].
La precisazione che l’attrazione della «tonica» si fa udire «nella misura in cui si dà l’occasione di far sentire la sua forza vincolante» non è in grado di spostare di molto l’asse principale di questo discorso, perché si dice qui soltanto non già che il modo in cui è costruito un pezzo pone in essere questa relazione, ma piuttosto se ne fa una questione di latenza che viene attualizzata: questa relazione vi è comunque, può accadere poi che nel brano - secondo le sue regole linguistiche - possano esservi circostanze più o meno favorevoli alla sua manifestazione.
Ma l’idea di una tonalità nascosta, che scorre come una sotterranea melodia [42] finisce con l’affermarsi anche nell’elaborazione più compiuta dell’idea di tonalità che non poggia solo sulla Serie 1, ma anche sulla nozione di Grundton introdotta in rapporto alla Serie 2.
È interessante notare a questo proposito che facendo riferimento a Rameau, Hindemith è disposto a salvare unicamente l’idea di basso fondamentale come idea di una linea musicale che non è effettivamente risuonante ma «che esiste solo nella rappresentazione del compositore e del fruitore». Precisamente egli scrive:
«Ma Rameau andò anche oltre. La sua teoria della tonalità nascondeva germi che nelle loro conseguenze erano destinati a crescere arditamente e direttamente sino alle nostre più recenti vedute. Secondo lui, le progressioni tonali vengono regolate attraverso il cosiddetto basso fondamentale. Questa è una linea del basso che esiste solo nella rappresentazione del compositore e del fruitore, non si tratta di una voce inferiore effettivamente risuonante. Con ciò viene dato al decorso musicale una base spirituale, in luogo di una base esclusivamente tecnica.... Stranamente tuttavia proprio questa idea così gravida di futuro venne dimenticata dai contemporanei di Rameau alla suo debutto. Ci si attenne agli aspetti più vistosi delle sue innovazioni e si trascurò quella che era realmente una geniale creazione. Solo ai nostri tempi essa rivive nuovamente come una delle idee guida della teoria della musica» [43].
Di questa idea del «basso fondamentale» che diventa qui l’idea di una struttura del pezzo che potrebbe non arrivare ad una effettiva manifestazione uditiva, Hindemith rivendica di essere erede nella propria proposta di rinnovamento della teoria musicale. In effetti, la «tonalità» di un brano secondo Hindemith va ricostruita portando alla luce un percorso di fondamentali (nel nuovo senso da lui proposto), attraverso una ricostruzione analitica che è tanto più è una produzione «spirituale» - per usare questa sua terminologia - quanto più ci muoviamo all’interno di unità linguistiche non riportabili direttamente al linguaggio tonale nell’accezione ristretta e storicamente determinata del termine.
Se rammentiamo l’intero percorso che abbiamo compiuto e la discussione che abbiamo via via sviluppato ci sembra di risentire anche in rapporto a questo problema quella oscillazione tra oggetti mentali e realtà musicale concreta che serpeggia un poco ovunque; quel contrasto che induce Hindemith da un lato a raggiungere, con la fisica, l’armonia delle sfere, dall’altro ad ammonire: «Per il musicista, che nella sua opera (Handwerk) nonostante l’inafferrabilità corporea del materiale, è un sano realista, i numeri e gli intervalli hanno valore soltanto quando li sente risuonare. Egli prende in considerazione il calcolo con proporzioni e curve solo se vede di poterne trarre vantaggi per il suo esercizio musicale pratico» [44].
Il risultato dell’applicazione della procedura di spostamento di grado alla composizione armonica del suono è stato duplice: non solo siamo pervenuti ad una scala dei gradi di affinità, ma attraverso la sistemazione delle loro frequenze in ordine progressivo, abbiamo estratto dall’unico suono fondamentale una scala di dodici note che è (nelle intenzioni di Hindemith) l’unica a poter rivendicare a buon diritto il nome di scala «naturale». Noi abbiamo trovato - rivendica Hindemith -«il metodo più semplice e più conseguente» che ci consente di trarre dalla successione degli armonici «la scala cromatica di dodici suoni» [45].
Questo punto di approdo non esclude la consapevolezza della molteplicità delle strutture scalari esistenti nella pratica musicale. L’esposizione di Hindemith si apre proprio mettendo in evidenza questa molteplicità:
«Un musicista intelligente, esperto nel suo mestiere, provvisto di conoscenze teoriche sufficienti, a cui chiedessimo quale ambito dei suoni percepibili, quali successioni ordinate di suoni egli ritenga costituire la più naturale, la più semplice e utilizzabile materia grezza su cui si esercita il lavoro tecnico di un compositore, indicherebbe senza dubbio, dopo breve riflessione, una scala, dal momento che senza scala non è pensabile alcuna musica secondo regole. In proposito egli penserà alle scale maggiori e minori, che sono l’inesauribile serbatoio per tutti i complessi sonori nei quali si possono ordinare tutte le melodie che gli sono note. Egli dimentica tuttavia che i nostri predecessori si servivano di altre scale e che anche oggi, presso popoli di altre culture, sono in uso serie di suoni che mostrano per molti riguardi ben poche somiglianze con le nostre» [46].
La pluralità linguistica è dunque data per acquisita. Ma viene anche da subito richiamata l’attenzione sul fatto che vi sono intervalli - come l’ottava e la quinta - che appaiono «inamovibili» (unverrückbar) all’orecchio in ogni cultura e questo fa pensare che la partizione determinata dall’ottava all’interno dell’intera fascia dei suoni musicalmente utilizzabili e la partizione dell’ottava attraverso la quinta, faccia parte del materiale sonoro grezzo (Tonrohstoff) [47] . Per Hindemith questo materiale non rimanda semplicemente al livello fenomenologico - al materiale sonoro concretamente percepito e non ancora musicalmente elaborato - ma al suo possibile sottostrato fisico. Certo, nel caso dei primi armonici questo sottostrato è anche, in certo senso, a portata di mano della percezione. A partire da questo spunto, ci si accinge allora ad un tentativo di trovare negli armonici una giustificazione per una partizione ben più ampia. La scala ottenuta, essendo l’unica deducibile secondo il metodo proposto è anche l’unica ad essere radicata negli armonici e dunque a poter essere anche caratterizzata come «naturale». Di fronte ad essa, tutte le altre scale sono da caratterizzare come «artificiali» - senza che questo peraltro pregiudichi la validità del loro impiego nell’espressione musicale o implichi una valutazione negativa su di esso. La scala naturale avrebbe il privilegio della «purezza» degli intervalli - ma nello stesso tempo questa purezza non è obbligatoriamente richiesta per ogni scopo espressivo. Le scale arabe, ad esempio, che si discostano liberamente dagli intervalli «naturali» sono «un materiale eccellente (vorzüglich) per la musica monofonica, puramente melodica» [48]. E vale in generale che nel caso di sviluppi melodici la deviazione dai rapporti naturali hanno spesso una forte connotazione espressiva. Entrando nel regno della polifonia e dell’armonia diventa invece importante la «purezza» dell’intervallo, anche se occorre contemperare con le esigenze armoniche, quelle melodiche che continuano a rivendicare i diritti ad una maggiore libertà:
«Non ogni scala che è stata escogitata in primo luogo per il lavoro melodico si piega facilmente alle esigenze dell’ordinamento armonico. Se una scala deve ubbidire ad entrambi gli scopi, allora gli intervalli debbono mostrare misure tali da porgere all’orecchio i suoni nella massima purezza (cioè, nella forma normale che la natura ci propone come modello nella regione inferiore della serie naturale dei suoni); d’altro lato la disposizione degli intervalli non deve essere così rigida da non ammettere tutte le piccole deviazioni dalla purezza naturale, deviazioni che per noi rappresentano gli stimoli principali dell’espressione melodica» [49] .
Vengono così rammentate le «note intenzionalmente crescenti o calanti» come «esempio estremo di suono impuro utilizzato da sempre come mezzo artistico», «la forma più lieve di deviazione dell’altezza, il vibrato», oltre un gran numero di «piccoli effetti melodici» come gradi intermedi [50] . L’inevitabile esattezza delle misure intervallari «dedotte» dalla serie degli armonici non deve dunque rispecchiarsi inesorabilmente nei fatti musicali. Al contrario è possibile che, per una ragione o per l’altra non vi sia mai una vera aderenza ad esse. Nel volume Komponist in seiner Welt Hindemith non esita a richiamare l’attenzione sul fatto che persino la scala naturale ha un gravissimo inconveniente, che è quello di non garantire nel caso del ritorno di una nota nominalmente identica l’identità dell’altezza. L’esempio seguente che egli propone illustra ciò che egli intende dire:

Se si attribuisce a do il valore 0 e si calcolano gli intervalli assunti nei loro valori «naturali» è facile rendersi conto che il do che chiude il motivo «cresce» di 22 cents [51] . Questo scarto potrebbe poi cumularsi in un eventuale sviluppo successivo, conducendo a risultati di intonazione intollerabili anche in un brano monofonico [52] . Rilievi di questo genere ed altri nella stessa direzione conducono Hindemith ad ammettere senz’altro che
«Con ciò non dobbiamo concludere che le misure delle nostre quinte, quarte, terze siano false - il dato di fatto della loro cantabilità è già una dimostrazione forte della loro giustezza - ma noi facciamo la singolare esperienza che nell’armonia e nella tonalità l’impiego di intervalli puri conduce immancabilmente a impurità» [53].
A rendere accettabili queste «impurità» inevitabili intervengono le tolleranze dell’orecchio, che sono, secondo Hindemith, particolarmente ampie. Ma queste considerazioni sono evidentemente aperte alle soluzioni più varie dal punto di vista musicale concreto: compreso il temperamento, che pur rappresentando un rischio, tuttavia viene caratterizzato come «una delle più geniali invenzioni dello spirito umano» [54].
Queste precisazioni sono opportune per evitare fraintendimenti, ma il punto più interessante sta nello stabilire il senso effettivo del fatto che il punto di arrivo sia rappresentato dalla scala cromatica. Come abbiamo osservato all’inizio, in passato era soprattutto il linguaggio tonale che veniva ad essere fine e tema di una giustificazione fisicalistica. Ma allora una «deduzione» - se non vuol limitarsi a richiamare l’attenzione sulla presenza della triade maggiore nei primi armonici - potrebbe tuttavia contentarsi del progetto di raggiungere le sette note della scala diatonica. La pretesa, qui perseguita con tanto accanimento, è invece stata quella di snocciolare tutti i dodici suoni - ed occorre rendersi chiaramente conto che questa circostanza non lascia le cose come sono proprio in rapporto al concetto stesso di «tonalità».
Al lettore che ha seguito pazientemente l’intero sviluppo e di cui si ode ora la sotterranea protesta: «Perché tutto questo? La scala cromatica non è per noi nulla di nuovo: non sarebbe forse stato più semplice considerarla come un dato di fatto fondamentale universalmente noto e risparmiarci calcoli che sono in ogni caso sgradevoli per un musicista?» [55], si replica appunto facendo notare che la deduzione delle dodici note, e non delle tre note della triade maggiore o delle sette della scala maggiore, ha il significato di attribuire alle alterazioni cromatiche, in precedenza considerate soprattutto come fioriture ed ornamenti relativamente marginali, lo statuto di note vere e proprie, allo stesso titolo di ogni altra, avendo anch’esse origine, secondo una unica regola, dallo stesso «genitore». Si tratta dunque di contestare la loro natura di alterazioni, ovvero di mere modificazioni espressive, per accoglierle sotto il dominio e le regole della «tonica».
«Tutte le teorie precedenti prendono le mosse dalla scala eptatonica diatonica maggiore e minore come materiale da costruzione (Baustein) delle creazioni musicali, esprimendo con ciò un’ opinione molto diffusa. Per mia esperienza l’annuncio di una diversa convinzione urta contro una dura resistenza da parte di musicisti ed amatori. Solo il compositore sa che le scale diatoniche da tempo hanno ceduto il dominio alla scala cromatica (...). Questa modificazione è ormai compiuta nel lavoro pratico, mentre manca ovunque ancora la comprensione di tutto ciò. La scala cromatica è certamente conosciuta, ma finora soltanto come ornamentazione o indebolimento della scala eptatonica. Ma chi si avvede della ricchezza del materiale sonoro offerta dalla scala cromatica e di quante goffe e poco chiare spiegazioni vengano a cadere con la sua assunzione come serie fondamentale per la teoria della musica, a lui dovrebbe accadere come ad uno che da sempre possedeva nella sua casa un estintore come un attrezzo inutilizzato e trascurato; solo nel caso di un incendio, quando le scale bruciano e non resta ormai altra possibilità che buttarsi dalla finestra, il valore dell’attrezzo sottovalutato viene riconosciuto e perciò apprezzato per il futuro. Noi abbiamo avuto esperienza nella musica di un simile incendio e siamo pieni di soddisfazione per aver riconosciuto come una salvezza la scala cromatica» [56].
Le modificazioni che intervengono a questo punto non sono facili da valutare in tutta la loro portata soltanto sulla base delle cose che abbiamo detto fin qui: è possibile tuttavia almeno segnalare gli aspetti principali. Se viene meno l’articolazione diatonica, la distinzione tra modo maggiore e minore non ha più carattere di architrave strutturale - ed una pratica compositiva che prenda le mosse di qui può contare su un impiego incondizionato delle dodici note che, sotto questo riguardo, hanno pari dignità.
Ci troviamo così di fronte ad una sorta di «dodecafonia tonale» che fa da esatto contraltare alla «dodecafonia atonale» di Schönberg [57] . Peraltro vi sono tra l’una e l’altra alcune rivendicazioni comuni non irrilevanti: in particolare l’idea della «scala cromatica» come una sorta di frame sovraordinato o sottoordinato alle suddivisioni diatoniche e quindi provvisto di un carattere di maggiore generalità, la rivendicazione dei dodici suoni come punto di arrivo di uno sviluppo, il richiamo al cromatismo del Tristano come importantissimo antecedente [58] , a cui si aggiunge, da parte di Hindemith un rimando significativo a Gesualdo da Venosa [59] . Sia Hindemith sia Schönberg non hanno alcun interesse per la musica etnica e per la musica extraeuropea in genere, ed entrambi non sono interessati ad una ripresa della problematica legata alla musica modale [60] .
Un elemento comune deve essere indicato anche nel fatto stesso di considerare il cromatismo puramente sotto il profilo dell’azione disgregante che esso esercita sull’ordine diatonico e nello stesso tempo di prevedere una determinazione rigida di ogni grado, e quindi anche delle note cromaticamente alterate. Nella prospettiva di entrambi cessa in realtà di aver senso la nozione stessa di alterazione cromatica, che è legata ad una struttura diatonica relativamente stabile rispetto alla quale i cromatismi debbono essere caratterizzati da una mobilità di principio. Naturalmente fa parte della tradizione colta europea la fissazione delle alterazioni cromatiche che si sono andate a sovrapporre alle alterazioni per trasposizione, che hanno una natura ed una funzione completamente diversa. Le posizioni di Hindemith e di Schönberg si situano sulla scia di questa tradizione; e per questo non viene avvertito nessun problema nel «dedurre» i luoghi delle alterazioni cromatiche come luoghi fissi come nel caso di Hindemith oppure, come nel caso di Schönberg, nel reperirli come tali dalla scala temperata. In coerenza con ciò, Schönberg prescrive che la serie «non deve essere in nessun grado identica alla scala cromatica» [61], e di conseguenza essa può avere al massimo uno o due semitoni in successione; a sua volta Hindemith ammonisce che assumere «la scala cromatica come fondamento (Grundlage) non significa che l’armonia e la melodia debbano abbandonarsi ad un eterno su e giù di lamentosi scivolamenti semitonali» [62], prendendo una posizione molto decisa contro l’impiego dei piccoli intervalli. Nel corso stesso della deduzione della Serie 1, quando ci si imbatte in una misura molto prossima ad un valore già ottenuto, ci si rifiuta di accettarla con l’argomento che un intervallo molto piccolo tende a presentarsi come ausiliario (Ableger) di un altro (osservazione in realtà assai acuta). Ma, obbietta Hindemith, se riteniamo ammissibile attribuire un ausiliario ad una nota singola, allora aprireremmo la strada ad una moltiplicazione a piacere di simili note ausiliarie, arrivando ad una suddivisione dell’ottava che sarebbe impraticabile [63] . Dubbi e perplessità vengono corrispondentemente mosse all’esperienze coeve di quartitonalismo [64] .
Ci si può chiedere tuttavia se muovendoci in questa direzione non scivoleremmo da un piano di discorso rivolto a questioni di ordine generale ad enunciazioni iniziali di un progetto espressivo che ha la sua naturale realizzazione nell’opera stessa di Hindemith. È indubbio che quando ci si richiama all’incendio che è intervenuto nella casa della musica ed alla possibilità di porre riparo ad esso attraverso la scelta dei dodici suoni si fa riferimento a nuove possibilità compositive - ed in rapporto ad esse non possiamo certo dire: qui le questioni di «stile» non entrano in linea di conto. Questo del resto, come si è già accennato in precedenza, è stato anche l’aspetto secondo cui è stata prevalentemente considerata la «parte speculativa» della Unterweisung di Hindemith. Più precisamente: questo è stato anche l’alibi per sentirsi autorizzati a voltar pagina, non solo sulla parte speculativa ma anche sugli elementi teorici ovunque affioranti nella parte didattica. Se si riducono le premesse teoriche a enunciazioni programmatiche rispetto ad uno stile compositivo, allora non vi è bisogno di riflettere più di tanto intorno ad esse, le si accettano come postulati, utili eventualmente a rendere conto dello stile compositivo hindemithiano. Ora, non vi è dubbio che le considerazioni teoriche siano intrecciate con idee che riguardano possibili tecniche compositive. Ma in questo intreccio si deve saper anche cogliere un progetto che punta in direzione di un rinnovamento delle problematiche di principio di una teoria della musica e dell’apprestamento di nuovi strumenti analitici e di un ripensamento dei concetti musicali di base.
Questo vale in particolare proprio per la nozione di «tonalità». Giudizi estremamente superficiali sono stati talora enunciati sulla base della semplice citazione di belle frasi di forte tensione polemica come quella che parla della triade maggiore che deve apparire «sia per le persone colte che per quelle semplici come uno dei grandiosi fenomeni della natura; semplice e potente come la pioggia, la neve, il vento» [65]. Il fatto è che proprio la triade maggiore non assolve da nessuna parte nel sistema teorico di Hindemith la funzione che essa assolve nella teoria classica della tonalità [66]: questa teoria viene semplicemente sconvolta dalla nozione di Grundton così come viene elaborata nel corso della discussione intorno alla Serie 2. L’intenzione esplicita è qui quella di una identificazione del significato degli intervalli considerati come tali all’infuori di un nesso linguistico-funzionale precostituito. Si perviene così al progetto di una tipologia - o come anche si dice ad una «fenomenologia di tutti gli accordi» [67]- che può servire come riferimento per una caratterizzazione che si estende ad ogni combinazione intervallare possibile. Indipendentemente da un giudizio sulla sua realizzazione, si tratta di un progetto che è motivato dalle esigenze della musica novecentesca e dall’enorme ampliamento della tavolozza degli accordi possibili che non sono più dominabili attraverso nozioni mediate dalla teoria classica della tonalità. Alla sua base vi è l’idea dell’esistenza di un Grundton riferito al semplice intervallo. «Non ho mai trovato in alcun manuale - dice Hindemith - l’affermazione secondo cui gli intervalli hanno un suono fondamentale» [68]- e questo è certo, perché questa affermazione contraddice tutta la concettualità che in un modo o nell’altro è legata a fil doppio al linguaggio tonale. Anzitutto viene soppressa la concezione dell’accordo come sovrapposizione di terze; viene rimessa in discussione la nozione di rivolto e quindi la distinzione tra accordo in posizione fondamentale e in posizione rivoltata; cambia infine il modo di concepire la nota fondamentale dell’accordo. La stessa terminologia dovrebbe essere profondamente modificata, così come ogni classificazione degli accordi e le spiegazioni relative ai loro rapporti.
Non si tratta dunque dunque di una pura e semplice ripresa del linguaggio tonale e della sua teoria. Piuttosto si potrebbe parlare di un rilancio della nozione di tonalità che si trova all’altezza dei tempi: esso viene compiuto a partire dall’interno della crisi del linguaggio tonale, e il suo primo gesto consiste proprio in una rimessa in questione della nozione di tonalità consolidata dalla tradizione. Come abbiamo già notato, dal punto di vista della teoria musicale siamo in presenza di un tentativo di smantellare l’impianto teorico fornito da Rameau al linguaggio tonale [69] per proporre un sistema teorico capace ancora di rendere conto di esso, ma anche di forme di espressione musicale che lo precedono storicamente o che lo seguono [70] .
La vecchia teoria armonica viene spesso indicata nel testo di Hindemith con il termine generico di Harmonielehre [71] .Non è certo un caso che questo sia anche il titolo del trattato di Schönberg. Va in effetti segnalato un sorta di curioso e ignorato paradosso della teoria musicale del novecento: Schönberg che appare dal punto di vista musicale più radicale di Hindemith scrive l’ultimo grande trattato di armonia tonale; dal punto di vista della riflessione teorica, egli guarda alla tradizione prevalentemente con gli occhi della tradizione, anche se questo stesso trattato intende apprestare le motivazioni evolutive che portano al superamento di essa. È invece il «conservatore» Hindemith che si volge alla tradizione con una fortissima istanza di rinnovamento dell’apparato dei concetti interpretativi e con una denuncia esplicita dell’inadeguatezza degli strumenti tradizionali di fronte ai nuovi sviluppi della musica novecentesca.
Note
[1] Si veda sull’argomento Quaderni della Civica Scuola di Musica di Milano, n. 27, giugno 2000 dedicato a Gérard Grisey, a cura di Andrea Melis. Inoltre: L. Fichet, Les Théories scientifiques de la musique, Vrin, Parigi, 1995, Musiques spectrales, pp. 313 sgg.
[2] P. Hindemith, Unterweisung im Tonsatz, B. Schött’s Söhne, Mainz 1937. Abbreviazione utilizzata nelle citazioni: U, I o II vol. È stata considerata anche l’edizione americana realizzata sulla edizione del 1940 (Craft of musical composition, New York, 1942-45).
[3] Un accenno a questa circostanza vi è anche in Hindemith quando dice che «la serie degli armonici im Rohzustande - allo stato grezzo - non è utilizzabile a causa delle distanze che diventano sempre più piccole dei singoli elementi» (U, I, p. 42).
[4] unheilvoll - U, I, 61.
[5] U, I, p. 41.
[6] Nel sistema temperato il si bemolle è pari a 1000 cents.
[7] U, I, p. 41.
[8] «Nessuna teoria della musica che si possa prendere sul serio ha fino ad oggi oltrepassato la serie da 1 a 16 e noi vedremo nel corso delle nostre ricerche che è sufficiente una sezione ancora più piccola della serie degli ipertoni per presentare tutti i rapporti tra i suoni che servono al lavoro musicale» (U, I, pp. 41-42)
[9] U, I, p. 51.
[10] Ediz. americana: A Composer’s World, Cambridge Mass., 1952. Ediz. tedesca, Zurigo 1959 (Abbr. qui utilizzata: Komponist)
[11] Komponist, p. 91.
[12] ivi, p. 92.
[13] Per ottenere un la a 440 Hz occorrerebbe prendere un do a 65,40 Hz. La scelta è spiegata da Hindemith dicendo che la misura di 64 Hz è la «la misura normale per le richerche fisiche» benché musicalmente si usi un do un po’ più acuto (U., I, p. 34).
[14] U., I, p. 51.
[15] «tonales Planetensystem», U, I, p. 52.
[16] Il quinto armonico viene considerato rispettivamente come terzo (320:3) e come quarto (320:4). - E. Costère, Mort ou transfiguration de l’harmonie, PUF, Parigi 1962, nota a questo proposito: «Ensuite intervient le La comme son fondamental de la succession ayant le Mi comme 3e son; et l’on est dejà en droit de se demander par quel mystère le Mi n’intervient qu’après, bien que le La n’entre en ligne de compte qu’en fonction de lui» (p. 33). Se Costère si sente in diritto di fare una domanda simile ciò significa che non ha compreso il metodo di spostamento di grado utilizzato da Hindemith. Ciò del resto è dimostrato da altri aspetti alquanto grossolani della sua critica: come quando indica come un arbitrio l’aver inserito il mi b «che è estraneo ai primi intervalli naturali della fondamentale do» oppure rileva una contraddizione nella posizione assegnata al si b che può essere spiegata «solo come una approssimazione del settimo suono di cui egli pretenderebbe di non tener conto» (p. 33) - per non dire del fatto che si fa confusione tra Serie 1 e Serie 2, presentando quest’ultima come se essa presentasse «l’ordre de parenté avec Do» (p. 32) ed ignorando bellamente che essa non è fondata negli armonici! Si tratta di errori inammissibili in una critica di carattere stroncatorio.
[17] U. I, p. 54.
[18] U, I, p. 56.
[19] Non è necessario considerare il secondo armonico perché da esso, per la ragione già esposta, non possiamo attenderci nulla di nuovo.
[20] U, I, p. 57
[21] «für unseren Zweck nicht geeignet», U, I, p. 58. Vengono respinti in particolare i valori 92,16 e 122,88. Accade addirittura che nell’edizione del 1937 si accetti come buono il valore 115,2 per il si bemolle e si rifiuti invece come «inadatto allo scopo» il valore 113,78 e che nell’edizione del 1940 questa valutazione venga esattamente invertita. Questa correzione ha certamente il vantaggio di rendere più omogenea la scala risultante, ma nulla forse più di questa correzione mostra come Hindemith intenda pilotare il calcolo verso un risultato voluto.
[22] U, I, p. 59.
[23] Dal terzo armonico di mi bem_76,8 considerato come quinto. Secondo L. Fichet, Les Théories scientifiques de la musique, Vrin, Parigi, 1995, p. 108 il rifiuto di questo valore, già nella seconda fase, è condizionato dall’intenzione di dare al tritono una posizione del tutto a parte: «Hindemith est très influencé par la façon dont est considéré le triton dans la musique traditionelle. Il cite même encore cette fameuse expression "Diabolus in musica" qui le désigne dans tant de théories. Il n’est don pas question pour lui de le laisser sur le même plan que d’autres intervalles beaucoup plus innocents comme les tons ou les septièmes. C’est sans doute pour cela qu’il rejette un Sol b issu directement des fils de Do_64. Il préférait que le triton ne soit pas un ordinaire "petit fils" mais plutôt un arrière petit fils, un "Urenkel" du Do_64 pour pouvoir établir une très nette difference hierarchique entre le Fa#/Sol b et les autres notes qui viennent d’arriver dans sa gamme». Si tratta di un’ipotesi interessante che mostra ancora, se fosse necessario, un filo conduttore preordinato in queste scelte. Il testo di Fichet tuttavia suggerisce che anche qui vi sarebbe un aspetto tradizionalista di Hindemith, mentre la concezione che Hindemith ha del tritono va ben oltre la frase fatta del Diabolus in musica: esso occupa una posizione chiave nel sistema che non ha alcun riscontro con la tradizione. Del tutto arbitraria ci sembra la critica di Fichet di una pretesa ed impossibile divisione dell’ottava in intervalli semitonali pari a 16/15 che è estranea all’impostazione di Hindemith.
[24] U, p. 61.
[25] U, p. 61
[26] Non mi sembra perciò di poter condividere l’opinione espressa da C. Deliège, «Nature culture: choix de parcours... De la théorie de Hindemith aux fondaments présumés de l’harmonie atonale», in«Ostinato rigore - Revue internationale d’études musicales», 6-7, 95/96, pp. 69-100, secondo il quale «l’illogisme de cette présentation provenait évidemment du recours au système de la résonance acoustique pour obtenir une échelle chromatique aussi proche que possible du témperament égal» (p. 77).
[27] Dice giustamente Fichet, op. cit., p. 103: «Mais cette façon de voir les choses est totalmente artificielle, elle ne correspond à aucun phénomène acoustique réell malgré l’emploi de la notion d’harmoniques. C’est un pur jeu sur les nombres...»
[28] J. Chailley parla di délire spéculatif e di veritable monstre in Eléments de Philologie musicale, Paris 1985, pp. 64-65). La critica è presente anche in Expliquer l’harmonie, Paris, 1967, pp. 62 -63. Si tratta di una valutazione che si potrebbe arrivare persino a condividere, se non fosse realmente delirante l’esposizione che Chailley compie della posizione di Hindemith. Di essa non mette conto di parlare.
[29] U, I, pp. 72-73.
[30] U, I, p. 73.
[31] U, I, p. 52. Un’altra immagine impiegata da Hindemith è quella del nucleo dell’atomo e del suo corteo di elettroni. p. 72
[32] U, I, 72.
[33] Anche la posizione della sesta che precede qui la terza non è estranea alla teoria musicale del passato. Ad esempio, la seconda tavola proposta da Mersenne dei gradi di consonanza presenta la sesta prima della terza; ed in Eulero sesta e terza maggiore vengono disposte ad un unico livello dei gradi di consonanza. Cfr. P. Bailhache, Une histoire de l’acoustique musicale, Paris 2001, p. 81 e p. 121.
[34] U, I, p. 73.
[35] U, I, p. 100.
[36] U, I, p. 100 («La successione dei valori disposta nella serie 2 solleva la questione del significato consonante o dissonante degli intervalli»).
[37] U, I, p. 101.
[38] U, I, p. 101.
[39] U, I, p. 71.
[40] U, II, 112-113.
[41] U, II, p. 114.
[42] Komponist, p. 106: « la tonalità va compresa come una melodia proiettata in grande».
[43] Komponist, p. 125.
[44] U, I, p. 83.
[45] U, I, p. 62.
[46] U, I, p. 31.
[47] U, I, p. 32.
[48] U, I, p. 45.
[49] p. 42.
[50] p. 42.
[51] 0 + 204 + 702 - 498 + 112 -498 = 22.
[52] Komponist, p. 109.
[53] ivi.
[54] U, I, p. 45.
[55] U, I, pp. 62-63.
[56] U, I, p. 63.
[57] Si tratta di designazioni forse discutibili, ma comunque efficaci per indicare sia l’opposizione che la relazione. Di dodécaphonisme tonale parla J. Viret, Hindemith et la musique ancienne, in «Ostinato rigore - Revue internationale d’études musicales», 6-7, 95/96, pp. 147-162: «Dans ces conditions le "tonalisme" de Hindemith me saurait apparaître autrement que comme une réaction face à l’ "atonalisme" schönbergien (p. 155)... L’appellation de "dodécaphonisme tonal" que l’on pourra employer pour résumer la démarche de Hindemith met bien en évidence cette double motivation. D’un côté c’est un dodécaphonisme comme celui de Schönberg: Hindemith estime qe’au XXe siècle la gamme régnante n’est plus l’échelle diatonique à sept degrés ma bien celle des douze demi-tons chromatiques. Néanmoins il récuse, d’un autre côté, l’amalgame effetué par Schönberg entre le dodécaphone et le concept atonal» (p. 158).
[58] «Nel Tristano di Wagner il dominio del maggiore-minore è messo da parte. In luogo della scala diatonica subentra inequivocabilmente la scala cromatica come fondamento di tutte le linee e i complessi sonori. Ma la rivoluzione venne troppo presto. La decisione e la consequenzialità con la quale questo passo audace venne fatto rimase allora senza seguito. Per decenni il Tristano rimase l’unica opera su base cromatica, nemmeno il suo creatore ha intrapreso una seconda volta una così potente avanzata nel nuovo territorio. Solo a cavallo del secolo comincia a realizzarsi il nuovo e più ampio mondo sonoro mostrato nel Tristano... Se noi oggi, riconsiderando la situazione, assumiamo definitivamente la scala cromatica come materiale di costruzione (Baumaterial), così facendo proseguiamo ciò che è stato cominciato ottanta anni fa » (U, I, p. 63 e 66).
[59] U, I, p. 65.
[60] Osserva ancora molto bene J. Viret, cit., pp. 154-155: «Il est curieux toutefois de constater que le lien très fort que Hindemith a voulu conserver et entretenir avec les musiques d’un passé largement conçu, et englobant notamment toute la musique médiévale depuis le grégorien, n’est jamais allé jusqu’à ce rétour au modal et donc au diatonism qui a eu lieu presque partout ailleurs à la même époque... Hindemith entend pour sa part opérer un compromis à première vue surprenant entre le langages passés (modalité, tonalité, monodie, polyphonie, harmonie) et le chromatisme dodécaphonique, compromis qu’il est le seul, il faut bien le dire, à avoir tenté et réussi grâce à son propre génie créateur. Or si Hindemith et Schönberg, par delà l’antagonisme de leurs démarches respectives, se rejoignent dans leur position commune fase à l’actualité revendiquée de l’échelle chromatique - alors que partout ailleurs les échelles modales sont à l’ordre du jour -, cela tient peut-être au fait que la tradition modale était morte depuis longtemps en terre germaniques tandis qu’en d’autres pays elle vivait souterrainement grâce au folklore ou au chant sacré, et pouvait donc y être revivifiée le moment venu». p. 159: «Son horizon musical, s’il s’étendait aux chants populaires allemands, n’allait point jusqu’à englober les musiques ethniques ou d’autres folklores musicaux»; benché, si aggiunga poco dopo, ricordi pentatonici e modali restino presenti in Hindemith per via dell’ «astuzia» consistente nel porre come principi primi «ad un tempo la scala cromatica in semitoni e le consonanze primordiali di quinta e di quarta» (p. 160).
[61] A. Schönberg, Composizione con dodici note, in Stile e idea, trad. it. di M. G. Moretti e L. Pestalozza, Milano1975, pp. 110.
[62] U, I, p. 63.
[63] U, I, p. 56.
[64] U, I, § 13, p. 66 sgg.
[65] U, I, p. 39.
[66] J. Viret, cit., p. 160: «Les deux ’séries’ (Reihen) structurales, l’une mélodiques et l’autre armonique, accumulent les douze sons chromatiques, mais ici come là c’est la quinte qui est en tête et le demi-ton et le triton en queue de leur ordonnance hiérarchique respective. Ainsi l’instabilité tonale des demi-tons chromatiques se voit résorbée dans le réseau stabilisateur des relations omniprésentes de quintes et de quartes, dont les combinaisons harmoniques jouent chez Hindemith un rôle structurateur plus important que le superpositions de tierces sur lesquelles se fonde l’harmonie classique».
[67] U, I, p. 121.
[68] U, p. 86.
[69] Il passo precedentemente citato (cfr. n. 44) sulla valutazione di Rameau da parte di Hindemith continua così: «Perciò si trascurarono generosamente le manifeste debolezze delle teorie ramiste, e da questa negligenza si sviluppò una teoria della composizione stranamente distorta. Essa si mantenne lungo l’intero diciannovesimo secolo ed è ancora oggi, con poche modificazioni, la base per l’insegnamento della composizione e delle discipline associate ad essa (Armonia, contrappunto, fuga e così via), rappresentando così, per via dei tempi mutati, una fonte di costante inquietudine per tutti gli insegnanti di teoria» (Komponist, p. 125).
[70] In effetti Hindemith non ha esitato a mostrare esemplificativamente l’applicabilità del metodo analitico suggerito dalla propria impostazione a brani appartenenti ad autori ed a epoche molte differenti (Guillaume de Machault, Bach, Stravinsky e Schönberg). Questa circostanza è interessante anzitutto perché mostra gli intenti di generalità del metodo, intenti che non sono affatto disprezzabili, come talora vengono presentati. Essa rappresenta anzi uno dei motivi di interesse del progetto hindemithiano, che riceve dalla fondazione fisicalistica ad un tempo uno stimolo ed una falsa giustificazione. Come le nostre orecchie possono ascoltare un brano di Machault ed apprezzarlo (sia pure questo apprezzamento soggiacente alle relatività storiche), così non è affatto privo di senso ritenere che si possano apprestare strumenti utili per la comprensione di linguaggi musicali di epoche anche molto distanti tra loro. Naturalmente si tratta di valutare in che misura la tematica hindemithiana nel suo insieme e nei suoi assi portanti, e quindi nel suo essere così ostinatamente imperniata sul concetto di tonalità sia pure in una nuova riformulazione, possa risultare efficace - e di questo è perfettamente lecito dubitare. A questa questione in ogni caso nessuna critica di dettaglio intorno alla pertinenza di questo o quell’esempio può dare una risposta soddisfacente. Ciò vale in particolare per la critica che E. Costère, op. cit., p. 30-31 rivolge all’analisi di Hindemith dell’esempio schönberghiano (op. 33a batt. 19-29).
[71] cfr. U, I, p. 122.
